Dreieck berechnen aus Basis und Winkel
Berechnung des Flächeninhalts eines Dreiecks aus Länge der Basis und 2 Winkel
Dreieck Rechner (Basis + 2 Winkel)
Trigonometrische Berechnung
Das Dreieck wird aus der Basis und den beiden anliegenden Winkeln berechnet.
Visualisierung
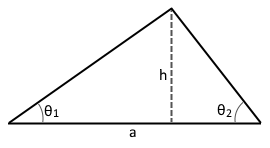
Das Diagramm zeigt ein Dreieck mit Basis a und den angrenzenden Winkeln θ₁ und θ₂.
Der dritte Winkel ergibt sich aus θ₃ = 180° - θ₁ - θ₂.
Was ist die Basis-Winkel-Methode?
Die Basis-Winkel-Methode ermöglicht die vollständige Dreiecksberechnung aus minimalen Angaben:
- Basis a: Eine bekannte Seitenlänge des Dreiecks
- Winkel θ₁, θ₂: Die beiden an der Basis anliegenden Winkel
- Dritter Winkel: Automatisch berechnet durch θ₃ = 180° - θ₁ - θ₂
- Trigonometrie: Berechnung über Sinus- und Tangens-Funktionen
- Anwendung: Ideal bei bekannten Winkelmessungen
- Vorteil: Vollständige Lösung aus drei Parametern
Trigonometrische Grundlagen
Die Methode basiert auf den fundamentalen Beziehungen der Trigonometrie:
Sinus-Regel
- Verhältnis von Seiten zu gegenüberliegenden Winkeln
- a/sin(α) = b/sin(β) = c/sin(γ)
- Ermöglicht Berechnung unbekannter Seiten
- Grundlage für Flächenberechnung
Tangens-Beziehungen
- Höhenberechnung über Tangens-Funktionen
- h = a × tan(θ₁) × tan(θ₂) / (tan(θ₁) + tan(θ₂))
- Direkte Beziehung zwischen Winkeln und Höhe
- Elegante Formel für komplexe Geometrie
Berechnungslogik verstehen
Die Berechnungsschritte folgen einer logischen trigonometrischen Sequenz:
1. Winkelkontrolle
Prüfung ob θ₁ + θ₂ < 180°, da sonst kein gültiges Dreieck entsteht
2. Seitenberechnung
Bestimmung der anderen Seiten über Sinusregel aus Basis und Winkeln
3. Flächenermittlung
Flächenberechnung über spezielle Formel mit Sinus-Produkten
Formeln für Basis-Winkel-Berechnung
Flächeninhalt
Spezielle Formel für Basis und zwei angrenzende Winkel
Höhe h
Höhe über Tangens-Beziehung
Dritter Winkel θ₃
\[\theta_3 = 180° - \theta_1 - \theta_2\]
Winkelsumme im Dreieck
Umfang P
Umfang über Sinusregel
Seitenlängen b, c
Weitere Seiten über Sinusregel
Alternative Flächenformeln
Symbole und Bezeichnungen
- A: Flächeninhalt des Dreiecks
- a: Basis (bekannte Seitenlänge)
- b, c: Weitere Seitenlängen
- h: Höhe zur Basis a
- θ₁, θ₂: Angrenzende Winkel zur Basis
- θ₃: Gegenüberliegender Winkel zur Basis
- P: Umfang des Dreiecks
- sin, tan: Trigonometrische Funktionen
Rechenbeispiel
Gegeben
1. Dritter Winkel
Rechtwinkliges Dreieck!
2. Flächenberechnung
Die Fläche beträgt etwa 24,63 Flächeneinheiten
3. Höhe berechnen
Höhe h ≈ 4,93 Einheiten
4. Weitere Seiten
Umfang P = 10 + 6,43 + 7,66 = 24,09
Kontrolle
A = ½ × 10 × 4,93 = 24,65 ✓
Pythagoras: 10² = 6,43² + 7,66² ✓
Dreiecksberechnung aus Basis und Winkeln in Theorie und Praxis
Die Basis-Winkel-Methode ist eine elegante trigonometrische Technik zur vollständigen Dreiecksbestimmung aus einer Seitenlänge und zwei angrenzenden Winkeln. Diese Methode kombiniert fundamentale Prinzipien der Trigonometrie mit praktischer Anwendbarkeit in Vermessung, Navigation und technischen Berechnungen.
Trigonometrische Grundlagen
Die Methode basiert auf den fundamentalen Beziehungen der Trigonometrie:
- Sinusregel: a/sin(α) = b/sin(β) = c/sin(γ) - ermöglicht Seitenberechnung
- Winkelsumme: α + β + γ = 180° - bestimmt den dritten Winkel automatisch
- Tangens-Beziehung: Direkte Höhenberechnung über tan(θ₁) und tan(θ₂)
- Flächenformel: Spezielle Ableitung für Basis-Winkel-Konfiguration
Mathematische Herleitung
Flächenformel-Entwicklung
Die spezielle Flächenformel A = (a²/2) × sin(θ₁)sin(θ₂)/sin(θ₁+θ₂) entsteht durch Kombination der klassischen Dreiecksfläche mit der Sinusregel und geometrischen Beziehungen der angrenzenden Winkel.
Höhenberechnung
Die Höhenformel h = a × tan(θ₁)tan(θ₂)/(tan(θ₁)+tan(θ₂)) ergibt sich aus der Zerlegung des Dreiecks in zwei rechtwinklige Teildreiecke mit der Höhe als gemeinsame Kathete.
Geometrische Interpretation
Die Basis teilt sich in zwei Abschnitte x und (a-x), wobei h/x = tan(θ₁) und h/(a-x) = tan(θ₂). Auflösung nach h führt zur Höhenformel.
Sinusregel-Anwendung
Aus der Sinusregel folgen direkt die Formeln für die weiteren Seiten: b = a×sin(θ₂)/sin(θ₁+θ₂) und c = a×sin(θ₁)/sin(θ₁+θ₂).
Praktische Anwendungen
Die Basis-Winkel-Methode findet breite Anwendung in verschiedenen Bereichen:
- Vermessungswesen: Triangulation, Geländeaufnahme, Grundstücksvermessung
- Navigation: Peilung, Standortbestimmung, Kursberechnungen
- Architektur: Dachkonstruktionen, Giebelberechnungen, Raumaufteilung
- Maschinenbau: Konstruktionsberechnung, Toleranzanalyse, Werkzeuggeometrie
- Astronomie: Parallaxenmessung, Entfernungsbestimmung, Winkelberechnungen
- Computergrafik: 3D-Modellierung, Perspektive, Polygon-Berechnungen
Berechnungsalgorithmus
Der systematische Berechnungsablauf folgt einer logischen Sequenz:
- Eingabevalidierung: Prüfung ob θ₁ + θ₂ < 180° (Dreiecksbedingung)
- Dritter Winkel: θ₃ = 180° - θ₁ - θ₂
- Seitenberechnung: b und c über Sinusregel aus a, θ₁, θ₂
- Höhenberechnung: h über Tangens-Formel
- Flächenberechnung: A über spezielle Basis-Winkel-Formel
- Umfangsberechnung: P = a + b + c
Besondere Fälle und Grenzbetrachtungen
Rechtwinkliges Dreieck
Wenn θ₁ + θ₂ = 90°, dann θ₃ = 90°. Die Formeln vereinfachen sich erheblich, da sin(90°) = 1 und spezielle rechtwinklige Beziehungen gelten.
Gleichschenkliges Dreieck
Bei θ₁ = θ₂ entstehen symmetrische Verhältnisse mit b = c und vereinfachten Formeln durch die Symmetrieeigenschaften.
Stumpfwinkliges Dreieck
Wenn θ₁ + θ₂ > 90°, wird θ₃ < 90°. Dies führt zu speziellen Überlegungen bei der Höhenberechnung und -position.
Grenzfälle
Bei θ₁ + θ₂ → 180° wird das Dreieck "entartet" (keine Fläche). Bei sehr kleinen Winkeln können numerische Stabilitätsprobleme auftreten.
Genauigkeit und Fehleranalyse
Bei der praktischen Anwendung sind verschiedene Aspekte der Genauigkeit zu beachten:
- Winkelmessgenauigkeit: Kleine Winkelfehler können große Auswirkungen haben
- Trigonometrische Genauigkeit: Rundungsfehler bei sin/tan-Berechnungen
- Numerische Stabilität: Probleme bei sehr spitzen oder sehr stumpfen Winkeln
- Fortpflanzung von Messfehlern: Ungenauigkeiten verstärken sich durch Berechnungskette
Vergleich mit anderen Methoden
Basis-Winkel
Gegeben: 1 Seite + 2 Winkel
Vorteil: Elegante Trigonometrie
Nachteil: Winkelmessung erforderlich
Drei Seiten
Gegeben: a, b, c
Vorteil: Nur Längenmessungen
Nachteil: Komplexere Formeln (Heron)
Zwei Seiten + Winkel
Gegeben: a, b + γ
Vorteil: Sinus-Formel
Nachteil: Mehrdeutigkeiten möglich
Historische Entwicklung
Die Basis-Winkel-Methode hat eine lange mathematische Geschichte:
- Antike Trigonometrie: Bereits Hipparchus und Ptolemäus verwendeten ähnliche Methoden
- Arabische Mathematik: Systematische Entwicklung der Sinusregel im Mittelalter
- Renaissance: Präzise trigonometrische Tafeln ermöglichten praktische Anwendungen
- Moderne Vermessung: Theodolite und GPS nutzen diese Prinzipien für Triangulation
Erweiterungen und Verallgemeinerungen
Die Grundprinzipien lassen sich auf komplexere Geometrien erweitern:
- Sphärische Trigonometrie: Dreiecke auf Kugeloberflächen (Navigation, Geodäsie)
- 3D-Geometrie: Tetraeder und räumliche Winkelberechnungen
- Vielecke: Zerlegung in Dreiecke für komplexe Polygone
- Numerische Verfahren: Computeralgorithmen für hochpräzise Berechnungen
Zusammenfassung
Die Basis-Winkel-Methode verbindet elegante Trigonometrie mit praktischer Anwendbarkeit. Sie ermöglicht die vollständige Dreiecksbestimmung aus minimalen Eingabedaten und bildet die Grundlage für viele Anwendungen in Vermessung, Navigation und technischen Berechnungen. Das Verständnis der zugrundeliegenden trigonometrischen Beziehungen und der numerischen Aspekte ist essentiell für eine erfolgreiche Anwendung in Wissenschaft und Technik.
|
|