Calculate Bessel-Ie Function

Online calculator for the exponentially scaled modified Bessel function Ieᵥ(z) - Numerically stable for large arguments

Bessel-Ie Function Calculator

Exponentially Scaled Bessel Function

The Ieᵥ(z) or exponentially scaled modified Bessel function provides numerical stability for large arguments.

Order number (integer)
Function argument (z > 0)
Result
Ieᵥ(z):

Bessel-Ie Function Curve

Mouse pointer on the graph shows the values.
The exponentially scaled form is numerically more stable for large z.

Why exponential scaling?

The exponentially scaled modified Bessel function solves numerical problems:

  • Numerical stability: Prevents overflow for large z
  • Exponential factor: Ieᵥ(z) = e^(-z) Iᵥ(z)
  • Precision: Maintains accuracy for all z ranges
  • Implementation: Standard in numerical libraries
  • Range extension: Computation for very large arguments
  • Robustness: Avoids machine precision problems

Numerical advantages over standard Bessel-I

The exponentially scaled version offers crucial numerical advantages:

Problem with standard Iᵥ(z)
  • Exponential growth ~ e^z
  • Overflow at z > ~700
  • Loss of precision
Solution through Ieᵥ(z)
  • Scaled range without overflow
  • Stable computation for all z
  • Preserved relative accuracy

Formulas for the Bessel-Ie Function

Definition
\[I_e\nu(z) = e^{-z} I_\nu(z)\]

Exponentially scaled modified Bessel function

Relationship to Iᵥ
\[I_\nu(z) = e^{z} I_e\nu(z)\]

Inversion of scaling

Series Expansion
\[I_e\nu(z) = e^{-z} \sum_{k=0}^{\infty} \frac{1}{k! \Gamma(k+\nu+1)} \left(\frac{z}{2}\right)^{2k+\nu}\]

Scaled power series

Asymptotic Form
\[I_e\nu(z) \sim \frac{1}{\sqrt{2\pi z}} \left(1 - \frac{4\nu^2-1}{8z} + \ldots\right)\]

For large z (without exponential growth)

Recurrence Formula
\[I_e{\nu-1}(z) - I_e{\nu+1}(z) = \frac{2\nu}{z} I_e\nu(z)\]

Same recurrence as unscaled version

Integral Representation
\[I_e n(z) = \frac{e^{-z}}{\pi} \int_0^\pi e^{z \cos \theta} \cos(n\theta) d\theta\]

For integer order n

Special Values

Important Values
Ie₀(0) = 1 Ie₁(0) = 0 Ie₀(1) ≈ 0.466
Symmetry Properties
I_e{-n}(z) = I_e n(z)

For integer n

Behavior at z = 0
\[I_e\nu(0) = \begin{cases} 1 & \text{if } \nu = 0 \\ 0 & \text{if } \nu > 0 \end{cases}\]

Same behavior as Iᵥ(0)

Application Areas

Numerical computations, large parameters, scientific computing, libraries.

Bessel-Ie vs. Bessel-I Comparison

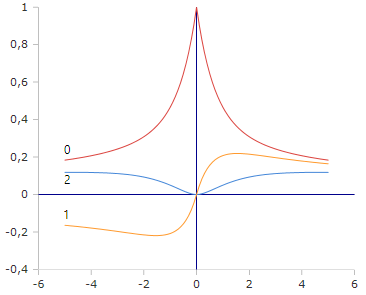
Bessel-Ie Functions
Bessel-Ie Functions (Order 0,1,2)

The exponentially scaled functions show controlled growth without numerical overflows even for large z values.

Characteristic Properties
  • Ie₀(z) starts at 1, then decreases
  • Ieₙ(z) with n > 0 starts at 0
  • Asymptotically: ~ 1/√(2πz)
  • No exponential overflows

Detailed Description of the Bessel-Ie Function

Mathematical Definition

The exponentially scaled modified Bessel function Ieᵥ(z) is a numerically stabilized version of the modified Bessel function Iᵥ(z). It was developed to solve the numerical problems of exponential growth.

Definition: Ieᵥ(z) = e^(-z) Iᵥ(z)
Using the Calculator

Enter the order ν (integer) and the argument z (positive real number). The Ie version is particularly suitable for large z values.

Numerical Background

The development of exponentially scaled Bessel functions was a response to the challenges of scientific computing. While Iᵥ(z) grows exponentially for large z and causes overflows, Ieᵥ(z) remains within controlled limits.

Properties and Applications

Numerical Applications
  • Scientific computing with large parameters
  • Numerical libraries (MATLAB, SciPy, GSL)
  • Simulation of physical systems
  • Statistical calculations
Mathematical Properties
  • Bounded growth for large z
  • Asymptotically: ~ 1/√(2πz)
  • Symmetry: Ie₋ₙ(z) = Ieₙ(z) for integer n
  • Monotonicity properties similar to standard version
Implementation Aspects
  • Libraries: Standard in modern math libraries
  • Precision: Maintained accuracy for all z ranges
  • Performance: Optimized algorithms available
  • Portability: Platform-independent implementations
Interesting Facts
  • The Ie functions are standard in IEEE floating-point implementations
  • For small z: Ieᵥ(z) ≈ e^(-z) (z/2)^ν / Γ(ν+1)
  • Algorithms often use continued fractions for higher efficiency
  • Important in Monte Carlo simulations with large parameters

Calculation Examples and Comparisons

Small Argument

z = 1:

I₀(1) ≈ 1.266

Ie₀(1) ≈ 0.466

Medium Argument

z = 10:

I₀(10) ≈ 2815.7

Ie₀(10) ≈ 0.1278

Large Argument

z = 100:

I₀(100) → Overflow

Ie₀(100) ≈ 0.0398

Computational Comparison

Standard Iᵥ(z) Problems

Exponential Growth:

I₀(50) ≈ 1.1 × 10²¹

I₀(100) ≈ 1.1 × 10⁴²

I₀(700) → Overflow

Problem: Numerical overflows significantly limit the usable range.

Ieᵥ(z) Solution

Controlled Behavior:

Ie₀(50) ≈ 0.0564

Ie₀(100) ≈ 0.0398

Ie₀(700) ≈ 0.0151

Advantage: Stable computation for arbitrarily large arguments.

Algorithmic Implementation

Numerical Methods
  • Continued Fractions: For large z and small ν
  • Miller's Algorithm: For medium z ranges
  • Series Expansion: For small z
  • Uniform Asymptotic: For large ν
Software Implementations
  • GSL: GNU Scientific Library
  • Boost: C++ Boost Math Library
  • SciPy: Python scientific computing
  • MATLAB: Built-in besseli function with scaling

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?


More special functions

Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Struve table • Modified Struve • Modified Struve table • Riemann Zeta