Calculate Bessel-Ye Function
Online calculator for the exponentially scaled Bessel function Yeᵥ(z) of the second kind - Numerically stable Neumann function with oscillation
Bessel-Ye Function Calculator
Exponentially Scaled Y-Function
The Yeᵥ(z) or exponentially scaled Bessel function shows numerical stability for complex arguments with singularity.
Bessel-Ye Function Curve
Mouse pointer on the graph shows the values.
The exponentially scaled form stabilizes oscillating behavior for complex arguments.
Why exponential scaling for the Y-function?
The exponentially scaled Bessel-Y function solves numerical challenges with complex arguments:
- Complex arguments: Stabilizes Im(z) ≠ 0 regions
- Exponential factor: Yeᵥ(z) = e^(-|Im(z)|) Yᵥ(z)
- Numerical robustness: Prevents overflow and underflow
- Singularity control: Managing the z=0 singularity
- Oscillation preservation: Maintains characteristic wave properties
- Algorithm stability: Optimized implementations
Scaled Neumann Function: Oscillation with Stability
The exponentially scaled Y-function combines oscillating behavior with numerical stability:
Standard Yᵥ(z) Problems
- Singularity at z = 0 complicates calculations
- Instabilities for complex arguments
- Numerical problems for large |Im(z)|
Yeᵥ(z) Advantages
- Controlled singularity through scaling
- Stable computation for complex z
- Preserved oscillation properties
Formulas for the Bessel-Ye Function
Definition
Exponentially scaled Bessel function of the second kind
Relationship to Yᵥ
Inversion of scaling
Asymptotic Form
For large z (scaled oscillation)
Recurrence Formulas
Same recurrence relations as standard Y-functions
Wronskian Determinant
Linear independence with scaled J-functions
Symmetry Property
For integer n
Behavior as z → 0
Scaled singularity at origin
Special Values
Important Values
Symmetry Properties
For integer n
Singularity at z = 0
For all ν > 0 (scaled)
Behavior as z → ∞
Scaled oscillation
Application Areas
Complex analysis, numerical stability, scaled radiation problems, robust algorithms.
Bessel-Ye vs. Bessel-Y Comparison
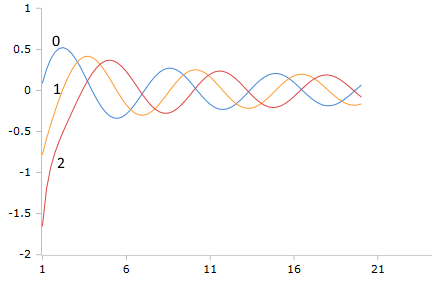
Bessel-Ye Functions (Order 0,1,2)
The exponentially scaled Y-functions show controlled singularities and stable oscillations without numerical instabilities for complex arguments.
Characteristic Properties
- Yeᵥ(z) → -∞ for z → 0⁺ (controlled singularity)
- Ye₀(z) ~ -(2/π) ln(z) for small z
- Asymptotically: ~ √(2/πz) sin(...) e^(-|Im(z)|)
- Numerically stable for complex arguments
Detailed Description of the Bessel-Ye Function
Mathematical Definition
The exponentially scaled Bessel function of the second kind Yeᵥ(z) is a numerically stabilized version of the Neumann function. It was developed to overcome the numerical challenges with complex arguments and the characteristic singularity.
Using the Calculator
Enter the order ν (integer) and the argument z (positive realle number). The Ye version is particularly suitable for numerical stability and complex analysis.
Numerical Background
The exponentially scaled Y-function was developed to solve the inherent numerical difficulties of the Neumann function, particularly the combination of singularity at z = 0 and oscillating behavior for complex arguments.
Properties and Applications
Numerical Applications
- Complex analysis with stable singularity handling
- Radiation problems with exponential stabilization
- Scientific computing with complex parameters
- Robust algorithms for oscillating systems
Mathematical Properties
- Controlled singularity through exponential scaling
- Oscillating behavior with stable amplitude
- Linear independence from scaled J-functions
- 90° phase shift relative to corresponding Je-functions
Implementation Aspects
- Libraries: Standard in modern math libraries
- Stability: Robust computation for complex z
- Performance: Optimized algorithms available
- Accuracy: Maintained precision in critical regions
Interesting Facts
- Ye-functions are essential for numerically stable Hankel functions
- The scaling eliminates problems for large |Im(z)| values
- Important in numerical solution of scattering problems
- Enables stable computation of Green's functions
Calculation Examples and Scaling Comparisons
Small Argument
z = 0.5:
Y₀(0.5) ≈ -0.445
Ye₀(0.5) ≈ -0.445
Medium Argument
z = 5:
Y₀(5) ≈ -0.309
Ye₀(5) ≈ -0.309
Complex Argument
z = 1 + 10i:
Y₀(z) → numerical problems
Ye₀(z) → stable computation
Numerical Stability in Detail
Standard Yᵥ(z) Challenges
Complex arguments:
Y₀(1 + 10i) → exponential growth
Y₀(10 + 10i) → overflow risk
Singularity at z = 0 amplifies problems
Problem: Exponential growth for large |Im(z)|.
Yeᵥ(z) Stabilization
Controlled behavior:
Ye₀(1 + 10i) → stable computation
Ye₀(10 + 10i) → controlled values
Scaled singularity manageable
Advantage: Stable computation for all complex arguments.
Physical Applications with Scaling
Scaled Radiation Problems
Complex wave propagation:
H_scaled(r,φ) = A Ye_m(kr) e^(imφ)
Numerically stable for damping media
Advantage: Stable computation even with strong damping.
Green's Functions
Scaled Green functions:
G_scaled(r,r') ∝ Ye₀(k|r-r'|)
Robust numerical implementation
Application: Numerically stable boundary integral equations.
Numerical Computation and Algorithms
Computation Methods
- Series Expansion: For medium z (scaled coefficients)
- Asymptotic Expansion: For large z (simplified by scaling)
- Recurrence Relations: Stable for all z ranges
- Miller's Algorithm: Adapted for scaled versions
Software Implementations
- GNU GSL: Optimized Ye-functions
- Boost Math: C++ template library with scaling
- SciPy: Python scipy.special.yve
- MATLAB: Built-in bessely with scaling option
|
|