Calculate Bessel-K Function
Online calculator for the modified Bessel function Kᵥ(z) of the second kind - Exponentially decaying solutions for physical systems
Bessel-K Function Calculator
Modified Bessel Function of the Second Kind
The Kᵥ(z) or modified Bessel function of the second kind shows exponentially decaying behavior and describes damped processes.
Bessel-K Function Curve
Mouse pointer on the graph shows the values.
The K-function shows exponentially decaying behavior for large z.
Why exponentially decaying behavior?
The modified Bessel function of the second kind differs fundamentally from the first kind:
- Exponential decay: Kᵥ(z) → 0 for z → ∞
- Singularity at z=0: Kᵥ(0) → ∞
- Physical damping: Describes diffusion and heat loss
- Complementary function: Partner to Iᵥ(z)
- Boundary value problems: Important for infinite domains
- Asymptotics: Kᵥ(z) ~ √(π/2z) e^(-z)
Physical applications of the Bessel-K function
The Bessel-K function is indispensable for damping and diffusion processes:
Heat Conduction
- Heat dissipation in infinite domains
- Steady-state temperature distributions
- Heat sinks and heat exchangers
Diffusion Processes
- Concentration gradients
- Mass transport in materials
- Porous media and filtration
Formulas for the Bessel-K Function
Definition
Definition via modified Bessel functions of the first kind
For integer ν
Limit definition for integer orders
Integral Representation
Integral form for Re(z) > 0
Asymptotic Form
For large z (exponential decay)
Recurrence Formula
Recurrence for adjacent orders
Symmetry Property
Symmetry with respect to order
Behavior as z → 0
Singularity at origin
Special Values
Important Values
Symmetry Properties
For all reellen ν
Singularity at z = 0
For all ν ≥ 0
Behavior as z → ∞
Exponential decay
Application Areas
Heat conduction, diffusion, electromagnetic shielding, quantum field theory.
Bessel-K Decay Behavior
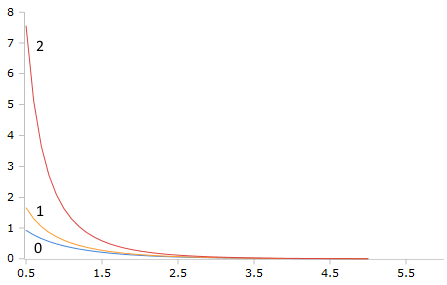
Bessel-K Functions (Order 0,1,2)
The K-functions show characteristic exponential decay with singularities at z = 0 and different decay rates depending on order.
Characteristic Properties
- Kᵥ(z) → ∞ for z → 0⁺
- Kᵥ(z) → 0 for z → ∞
- Asymptotically: ~ √(π/2z) e^(-z)
- Monotonically decreasing for all z > 0
Detailed Description of the Bessel-K Function
Mathematical Definition
The modified Bessel function of the second kind Kᵥ(z) is the second linearly independent solution of the modified Bessel differential equation. Unlike Iᵥ(z), it shows exponentially decaying behavior and is singular at z = 0.
Using the Calculator
Enter the order ν (integer) and the argument z (positive real number). The K-function is only defined for z > 0 due to the singularity at z = 0.
Physical Background
The Bessel-K functions describe damping and decay processes in cylindrical geometries. They are particularly important for problems with infinite boundary conditions, where physical quantities must vanish at infinity.
Properties and Applications
Physical Applications
- Heat conduction in infinite cylindrical media
- Diffusion processes with boundary conditions at infinity
- Electromagnetic shielding and skin effect
- Quantum field theory and particle physics
Mathematical Properties
- Exponential decay for large z
- Singularity at z = 0
- Symmetry: K₋ᵥ(z) = Kᵥ(z)
- Monotonically decreasing for all z > 0
Numerical Aspects
- Stability: Numerically challenging for small z
- Algorithms: Special methods for different z ranges
- Accuracy: High precision for large z
- Efficiency: Recurrence formulas for adjacent orders
Interesting Facts
- K₀(z) is important for logarithmic potentials in 2D
- K₁(z) appears in relativity theory for thermal equilibria
- K-functions are essential for Green's functions in physics
- They describe the behavior of fields at large distances
Calculation Examples and Decay Behavior
Small Argument
z = 0.5:
K₀(0.5) ≈ 0.924
K₁(0.5) ≈ 1.656
Medium Argument
z = 2:
K₀(2) ≈ 0.114
K₁(2) ≈ 0.140
Large Argument
z = 10:
K₀(10) ≈ 1.78×10⁻⁵
Strong exponential decay
Detailed Physical Applications
Heat Conduction
Steady-state heat conduction:
T(r) = A K₀(r/λ) for cylindrical heat source
λ is the characteristic length
Example: Heat sink with exponentially decaying temperature.
Electromagnetism
Skin effect:
E(r) ∝ K₀(r/δ) in conductive medium
δ is the skin depth
Example: Electromagnetic shielding and penetration depth.
Mathematical Properties and Relations
Asymptotic Behavior
For large z:
Kᵥ(z) ~ √(π/2z) e^(-z)
For small z (ν > 0):
Kᵥ(z) ~ Γ(ν)/2 (2/z)^ν
Special case: K₀(z) ~ -ln(z) for small z.
Relations to Other Functions
Wronskian determinant:
W[Iᵥ, Kᵥ] = -1/z
Relation to Hankel functions:
Kᵥ(z) = (π/2)i^(ν+1) H^(1)_ν(iz)
Significance: Fundamental solution system with Iᵥ(z).
Special Orders and Limiting Cases
Order ν = 0
K₀(z) - Fundamental solution:
Logarithmic singularity at z = 0
Application: 2D problems, logarithmic potentials.
Order ν = 1
K₁(z) - Derivative of K₀:
Important for gradient problems
Application: Diffusion fluxes, thermal gradients.
Numerical Computation and Algorithms
Computation Methods
- Series Expansion: For small z (with care at singularity)
- Asymptotic Expansion: For large z ≥ 15
- Recurrence Relations: For adjacent orders
- Continued Fractions: For medium z ranges
Software Implementations
- GNU GSL: High-precision K-functions
- Boost Math: C++ template library
- SciPy: Python scipy.special.kv
- MATLAB: Built-in besselk function
|
|