Calculate Bessel-Je Function

Online calculator for the exponentially scaled Bessel function Jeᵥ(z) of the first kind - Numerically stable oscillating cylindrical function

Bessel-Je Function Calculator

Exponentially Scaled Bessel Function

The Jeᵥ(z) or exponentially scaled Bessel function shows stable oscillating behavior as a cylindrical function.

Order number (integer)
Function argument (z > 0)
X-axis scaling
Result
Jeᵥ(z):

Bessel-Je Function Curve

Mouse pointer on the graph shows the values.
The exponentially scaled form eliminates amplitude growth for large z.

Why oscillating behavior instead of exponential growth?

The standard Bessel function differs fundamentally from modified Bessel functions:

  • Periodic oscillation: Jᵥ(z) oscillates for large z
  • Damping amplitude: Amplitude ~ 1/√z
  • Physical waves: Describes vibration and wave processes
  • Cylindrical symmetry: Solutions in cylindrical coordinates
  • Zeros: Infinitely many zeros for large z
  • Asymptotics: Jᵥ(z) ~ √(2/πz) cos(z - πν/2 - π/4)

Applications in wave problems and cylindrical symmetry

The Bessel-Je function is the numerically stable solution for oscillating wave processes:

Mechanical Vibrations
  • Circular membrane vibrations
  • Cylinder and tube vibrations
  • Acoustic resonators
Electromagnetic Waves
  • Cylindrical waveguides
  • Antenna radiation
  • Cavity resonators

Formulas for the Bessel-Je Function

Definition
\[J_e\nu(z) = e^{-|Im(z)|} J_\nu(z)\]

Exponentially scaled Bessel function

Relationship to Jᵥ
\[J_\nu(z) = e^{|Im(z)|} J_e\nu(z)\]

Inversion of scaling

Series Expansion
\[J_e\nu(z) = e^{-|Im(z)|} \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Scaled power series

Asymptotic Form
\[J_e\nu(z) \sim \sqrt{\frac{2}{\pi z}} \cos\left(z - \frac{\nu\pi}{2} - \frac{\pi}{4}\right) e^{-|Im(z)|}\]

For large z (with stable amplitude)

Recurrence Formula
\[\frac{2\nu}{z} J_e\nu(z) = J_e{\nu-1}(z) + J_e{\nu+1}(z)\]

Same recurrence as unscaled version

Integral Representation
\[J_e n(z) = \frac{e^{-|Im(z)|}}{\pi} \int_0^\pi \cos(z \sin \theta - n\theta) d\theta\]

For integer order n

Special Values

Important Values
Je₀(0) = 1 Je₁(0) = 0 Je₀(π) ≈ 0.0633
Symmetry Properties
J_e{-n}(z) = (-1)^n J_e n(z)

For integer n

Behavior at z = 0
\[J_e\nu(0) = \begin{cases} 1 & \text{if } \nu = 0 \\ 0 & \text{if } \nu > 0 \end{cases}\]

Same behavior as Jᵥ(0)

Application Areas

Wave propagation, vibration problems, cylindrical geometry, antenna design.

Bessel-Je Oscillation Pattern

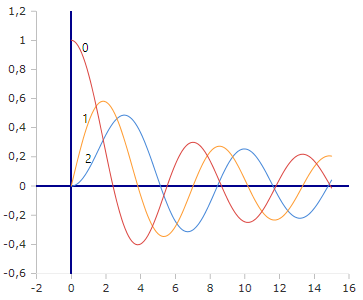
Bessel-Je Functions
Bessel-Je Functions (Order 0,1,2)

The exponentially scaled functions show clear oscillations with controlled amplitude without numerical instabilities.

Characteristic Properties
  • Je₀(z) starts at 1, then oscillates
  • Jeₙ(z) with n > 0 starts at 0
  • Asymptotically: ~ √(2/πz) cos(...)
  • Stable amplitude through scaling

Detailed Description of the Bessel-Je Function

Mathematical Definition

The exponentially scaled Bessel function Jeᵥ(z) is a numerically stabilized version of the standard Bessel function Jᵥ(z). Unlike modified Bessel functions, it retains the oscillating behavior but eliminates numerical instabilities.

Definition: Jeᵥ(z) = e^(-|Im(z)|) Jᵥ(z)
Using the Calculator

Enter the order ν (integer) and the argument z (positive real number). The graph stretch parameter controls the X-axis scaling for better visualization.

Physical Background

Bessel functions were originally developed by Friedrich Bessel for astronomical calculations. They describe wave propagation in cylindrical systems and are fundamental to many physical phenomena.

Properties and Applications

Physical Applications
  • Circular membrane vibrations (drum head)
  • Electromagnetic waves in cylindrical conductors
  • Acoustic resonators and cavities
  • Diffraction at cylindrical objects
Mathematical Properties
  • Oscillating behavior for large z
  • Damping amplitude ~ 1/√z
  • Symmetry: Je₋ₙ(z) = (-1)ⁿ Jeₙ(z) for integer n
  • Infinitely many zeros for z > 0
Numerical Aspects
  • Stability: Numerically stable for complex arguments
  • Scaling: Eliminates exponential growth for Im(z) ≠ 0
  • Accuracy: Maintained precision in all z ranges
  • Efficiency: Optimized algorithms available
Interesting Facts
  • Bessel functions describe the vibration modes of drums
  • The zeros of J₀(z) determine resonance frequencies of cylindrical cavities
  • Bessel functions are essential for the Fourier-Bessel transform
  • They appear in quantum mechanics for radially symmetric problems

Calculation Examples and Oscillation Properties

Small Argument

z = π/2:

J₀(π/2) ≈ 0.567

Je₀(π/2) ≈ 0.567

First Zero

z ≈ 2.405:

J₀(2.405) ≈ 0

Je₀(2.405) ≈ 0

Large Argument

z = 20:

J₀(20) ≈ 0.167

Je₀(20) ≈ 0.167

Wave Applications and Cylindrical Symmetry

Acoustic Applications

Drum head vibrations:

Radial modes: u(r,φ,t) = J₀(k·r) cos(ωt)

Zeros determine resonance frequencies

Example: Circular membrane with radius R has resonances at k·R = zeros of J₀.

Electromagnetic Waves

Cylindrical waveguides:

TM modes: E_z ∝ J_m(k_c·r) e^(imφ)

Cutoff frequencies through Bessel zeros

Example: TE₀₁ mode in waveguide has lowest cutoff frequency.

Zeros and Oscillation Behavior

Important Zeros

J₀(z) zeros:

2.405, 5.520, 8.654, 11.792, ...

J₁(z) zeros:

3.832, 7.016, 10.173, 13.324, ...

Asymptotics: Zeros follow αₙ ≈ (n - 1/2)π for large n.

Oscillation Properties

Asymptotic behavior:

Jᵥ(z) ~ √(2/πz) cos(z - νπ/2 - π/4)

Period ≈ 2π, amplitude ~ 1/√z

Properties: Oscillation frequency remains constant, only amplitude decreases.

Numerical Computation and Algorithms

Computation Methods
  • Series Expansion: For small |z| and small ν
  • Asymptotic Expansion: For large |z|
  • Recurrence Relations: For adjacent orders
  • Continued Fractions: For special ranges
Software Implementations
  • GNU GSL: Highly accurate implementations
  • Boost Math: C++ template library
  • SciPy: Python scipy.special.jn
  • MATLAB: Built-in besselj function

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?


More special functions

Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Struve table • Modified Struve • Modified Struve table • Riemann Zeta