Calculate Bessel-J Function

Online calculator for the Bessel function Jᵥ(z) of the first kind - Classical oscillating cylindrical function for wave processes

Bessel-J Function Calculator

Classical Bessel Function

The Jᵥ(z) or classical Bessel function shows oscillating behavior and is the foundation of all cylindrical functions.

Order number (integer)
Function argument (z > 0)
X-axis scaling
Result
Jᵥ(z):

Bessel-J Function Curve

Mouse pointer on the graph shows the values.
The classical Bessel function shows characteristic oscillations with damping amplitude.

Characteristic oscillations of the Bessel-J function

The classical Bessel function is the original and most important cylindrical function:

  • Periodic oscillation: Jᵥ(z) oscillates for large z
  • Damping amplitude: Amplitude ~ 1/√z
  • Infinite zeros: Regularly distributed zeros
  • Fundamental importance: Basis of all other Bessel functions
  • Physical relevance: Direct solution of the wave equation
  • Asymptotics: Jᵥ(z) ~ √(2/πz) cos(z - πν/2 - π/4)

Fundamental solution in cylindrical coordinates

The Bessel-J function is the fundamental solution of the Bessel differential equation:

Bessel Differential Equation
\[z^2 \frac{d^2 y}{dz^2} + z \frac{dy}{dz} + (z^2 - \nu^2)y = 0\]

Fundamental ODE of cylindrical functions

General Solution
\[y(z) = C_1 J_\nu(z) + C_2 Y_\nu(z)\]

J and Y form a fundamental solution system

Formulas for the Bessel-J Function

Series Expansion
\[J_\nu(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Fundamental power series expansion

Symmetry Relation
\[J_{-\nu}(z) = (-1)^\nu J_\nu(z)\]

For integer ν

Asymptotic Form
\[J_\nu(z) \sim \sqrt{\frac{2}{\pi z}} \cos\left(z - \frac{\nu\pi}{2} - \frac{\pi}{4}\right)\]

For large z (leading term of asymptotic expansion)

Recurrence Formulas
\[\frac{2\nu}{z} J_\nu(z) = J_{\nu-1}(z) + J_{\nu+1}(z)\] \[\frac{d}{dz} J_\nu(z) = \frac{1}{2}[J_{\nu-1}(z) - J_{\nu+1}(z)]\]

Recurrence relations for efficient computation

Integral Representation
\[J_n(z) = \frac{1}{\pi} \int_0^\pi \cos(z \sin \theta - n\theta) d\theta\]

For integer order n (Bessel integral)

Generating Function
\[e^{\frac{z}{2}(t - \frac{1}{t})} = \sum_{n=-\infty}^{\infty} J_n(z) t^n\]

Laurent expansion of the generating function

Special Values

Important Values
J₀(0) = 1 J₁(0) = 0 J₀(π) ≈ -0.305
Symmetry Properties
J_{-n}(z) = (-1)^n J_n(z)

For integer n

Behavior at z = 0
\[J_\nu(0) = \begin{cases} 1 & \text{if } \nu = 0 \\ 0 & \text{if } \nu > 0 \end{cases}\]

Limiting behavior at origin

Zeros of J₀
2.405, 5.520, 8.654, 11.792, 14.931, ...

First zeros of the fundamental mode

Application Areas

Membrane vibrations, waveguides, acoustic resonators, antenna theory.

Bessel-J Oscillation Pattern

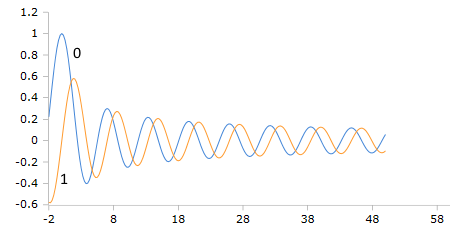
Bessel-J Functions
Bessel-J Functions (Order 0,1)

The classical Bessel functions show characteristic oscillations with decreasing amplitude proportional to 1/√z for large arguments.

Characteristic Properties
  • J₀(z) starts at 1, first zero at z ≈ 2.405
  • J₁(z) starts at 0, first zero at z ≈ 3.832
  • Asymptotically: ~ √(2/πz) cos(...)
  • Oscillation period ≈ 2π for large z

Detailed Description of the Bessel-J Function

Mathematical Definition

The classical Bessel function Jᵥ(z) is the fundamental solution of the Bessel differential equation. It was originally developed by Friedrich Bessel during the analysis of planetary motion and is today the most important cylindrical function.

Fundamental Property: Jᵥ(z) is the everywhere regular solution of the Bessel ODE
Using the Calculator

Enter the order ν (integer) and the argument z (positive real number). The graph stretch parameter controls the X-axis scaling for optimal oscillation display.

Historical Background

Friedrich Bessel (1784-1846) originally developed these functions for astronomical calculations. The functions proved to be fundamental for all problems with cylindrical symmetry and are today indispensable in physics and engineering.

Properties and Applications

Physical Applications
  • Circular membrane vibrations (drum head, loudspeakers)
  • Electromagnetic waves in cylindrical waveguides
  • Acoustic resonators and cavity resonators
  • Diffraction of electromagnetic waves at cylinders
Mathematical Properties
  • Oscillating behavior with damping amplitude
  • Infinitely many zeros for ν ≥ 0
  • Orthogonality relations on intervals
  • Complete function system for cylindrical problems
Numerical Aspects
  • Stability: Numerically stable for all real z ≥ 0
  • Algorithms: Different methods depending on z range
  • Accuracy: High precision through optimized implementations
  • Efficiency: Recurrence formulas for adjacent orders
Interesting Facts
  • J₀(z) describes the fundamental vibration of a circular membrane
  • The zeros determine resonance frequencies of cylindrical cavities
  • Bessel functions are essential for the Fourier-Bessel transform
  • They enable the solution of the wave equation in cylindrical coordinates

Calculation Examples and Oscillation Behavior

Small Argument

z = 1:

J₀(1) ≈ 0.765

J₁(1) ≈ 0.440

First Zero

z ≈ 2.405:

J₀(2.405) ≈ 0

First zero of J₀

Large Argument

z = 20:

J₀(20) ≈ 0.167

Asymptotic behavior

Physical Applications in Detail

Membrane Vibrations

Circular membrane:

u(r,φ,t) = J_m(k·r) cos(mφ) cos(ωt)

Resonances at J_m(k·R) = 0

Example: Drum head with radius R has fundamental frequency at k·R = 2.405.

Electromagnetic Waves

Cylindrical waveguides:

E_z ∝ J_m(k_c·r) e^(imφ) e^(ikz)

Cutoff at J_m(k_c·a) = 0

Example: Coaxial cables and waveguides use these modes.

Zeros and Special Properties

Zeros of First Orders

J₀(z) zeros:

2.405, 5.520, 8.654, 11.792, 14.931, ...

J₁(z) zeros:

3.832, 7.016, 10.173, 13.324, 16.471, ...

Asymptotics: Zeros follow αₙ ≈ (n + ν/2 - 1/4)π for large n.

Asymptotic Behavior

For large z:

Jᵥ(z) ~ √(2/πz) cos(z - νπ/2 - π/4)

Amplitude ~ 1/√z, period ≈ 2π

Properties: Damped oscillation with constant frequency.

Orthogonality and Fourier Series

Orthogonality Relation

On interval [0,R]:

\[\int_0^R r J_\nu\left(\frac{\alpha_{\nu,m} r}{R}\right) J_\nu\left(\frac{\alpha_{\nu,n} r}{R}\right) dr = 0\]

for m ≠ n

Significance: Enables Fourier-Bessel expansions.

Fourier-Bessel Series

Expansion of function f(r):

\[f(r) = \sum_{n=1}^{\infty} A_n J_\nu\left(\frac{\alpha_{\nu,n} r}{R}\right)\]

with coefficients A_n

Application: Solution of boundary value problems in cylinders.

Numerical Computation and Algorithms

Computation Methods
  • Series Expansion: For small |z| ≤ 8
  • Asymptotic Expansion: For large |z| ≥ 25
  • Recurrence Relations: For medium ranges
  • Chebyshev Approximation: For transition regions
Software Implementations
  • GNU GSL: High-precision implementations
  • Boost Math: C++ template library
  • SciPy: Python scipy.special.jv
  • MATLAB: Built-in besselj function

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?


More special functions

Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Struve table • Modified Struve • Modified Struve table • Riemann Zeta