Exponentially Scaled Bessel-Ie Function for Complex Numbers

Calculation of the exponentially scaled modified Bessel function \(I_e(z) = e^{-|z|} I_\nu(z)\) of the first kind

Bessel-Ie Function Calculator

Exponentially Scaled Bessel Function \(I_e(z)\)

The exponentially scaled Bessel function \(I_e(z) = e^{-|z|} I_\nu(z)\) prevents numerical overflows for large arguments and is especially useful for numerical calculations with large values.

Complex Argument z = a + bi
+
i
Integer or rational order of the Bessel function
Calculation Result
\(I_e(z)\) =

Bessel-Ie Properties

Scaling

Exponential

Factor: \(e^{-|z|}\)

Prevents overflow
Base

Bessel-I

Type: \(I_\nu(z)\)

Modified function
Order

ν ∈ ℝ

Any real number

Integer or rational
Argument

z ∈ ℂ

Complex: a+bi

Real and imaginary part
Important Properties
  • Numerically stable calculation for large |z|
  • Prevents exponential overflow
  • Defined as: \(I_e(z) = e^{-|z|} I_\nu(z)\)
  • Asymptotically: \(I_e(z) \sim \frac{1}{\sqrt{2\pi|z|}}\) for |z| → ∞
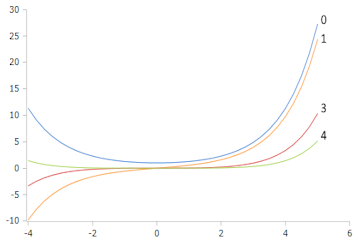
BesselI

Plot of the Bessel-I function (before exponential scaling)

Definition of the Exponentially Scaled Bessel Function

The exponentially scaled modified Bessel function \(I_e(z)\) is defined as:

Scaled Definition
\[I_e(z) = e^{-|z|} I_\nu(z) = e^{-|z|} \sum_{m=0}^{\infty} \frac{1}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Exponentially scaled version to avoid numerical overflows

Numerical Stability
\[|I_e(z)| \leq \frac{C}{\sqrt{|z|}}\]

Bounded for large |z|, prevents overflow

Relationship to Bessel-I
\[I_\nu(z) = e^{|z|} I_e(z)\]

Back-transformation to the original function

Important Properties of the Scaled Bessel Function

Asymptotic Behavior
\[I_e(z) \sim \frac{1}{\sqrt{2\pi|z|}} \quad \text{for } |z| \to \infty\]

Constant asymptotic behavior without exponential growth

Numerical Advantages
\[\max|I_e(z)| < \infty \quad \text{for all } z\]

Bounded values prevent overflow problems

Scaling Factor
\[s(z) = e^{-|z|} = e^{-\sqrt{\text{Re}(z)^2 + \text{Im}(z)^2}}\]

Exponential damping factor based on the modulus of z

Recurrence Relations
\[I_{e,\nu-1}(z) - I_{e,\nu+1}(z) = \frac{2\nu}{z} I_{e,\nu}(z)\]

Scaled recurrence relations apply analogously

Applications of the Scaled Bessel Function

Numerical Analysis
Large arguments Overflow prevention Stable algorithms Precise calculation
Scientific Computing
Monte Carlo Methods:
Statistical simulations
Random processes
Financial Models:
Option pricing
Risk modeling
Signal Processing

Filter design

Spectral analysis

Beamforming

Physical Models

Diffusion equations

Heat conduction models

Quantum field theory

Scattering theory

Exponentially Scaled Bessel Functions - Detailed Description

Numerical Stability

The exponentially scaled Bessel function \(I_e(z)\) was specifically developed to solve the numerical problems of the ordinary modified Bessel function \(I_\nu(z)\) for large arguments.

Problem Statement:
• \(I_\nu(z)\) grows exponentially for large |z|
• Numerical overflows for |z| > 700
• Loss of precision in calculations
• Unstable algorithms

Solution Approach

By the definition \(I_e(z) = e^{-|z|} I_\nu(z)\), the exponentially growing part is "divided out", so that the resulting function remains numerically stable.

Advantages of Scaling

Without scaling: \(I_\nu(100)\) ≈ 10⁴³ (overflow)
With scaling: \(I_{e,\nu}(100)\) ≈ 0.056 (stable)

Mathematical Properties

The scaled function retains all important mathematical properties of the original Bessel function, but is numerically much more stable.

Preserved Properties:
• Recurrence relations remain valid
• Differential equations analogous
• Symmetry relations persist
• Integral representations possible

Implementation

In numerical practice, the scaled version is used and the result is back-transformed if needed:

\[I_\nu(z) = e^{|z|} \cdot I_e(z)\]

Back-transformation only when explicitly needed

Computer Implementation

Modern libraries use the scaled version automatically and handle the scaling transparently for the user.

Comparison: Scaled vs. Unscaled

Unscaled Bessel-I Function
Definition: \(I_\nu(z)\)
Behavior: Exponential growth
Problems: Overflow for large |z|
Limit: |z| ≲ 700 (double precision)
Scaled Bessel-Ie Function
Definition: \(I_e(z) = e^{-|z|} I_\nu(z)\)
Behavior: Asymptotically constant
Advantages: No overflow
Range: All |z| (practically unlimited)
Practical Application Guidelines
  • Small |z| ≤ 10: Both versions usable
  • Medium |z| ≤ 100: Scaled version recommended
  • Large |z| > 100: Only use scaled version
  • Iterative algorithms: Always scaled version
  • Scientific libraries: Automatic choice
  • Special functions: Transparent scaling

Bessel Functions - Complete Definitions and Scaling

Modified Bessel Functions

The modified Bessel function of the first kind of order n is defined as:

\[I_{\nu}(z) = \sum_{m=0}^{\infty} \frac{1}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

The exponentially scaled version is:

\[I_e(z) = e^{-|z|} I_{\nu}(z)\]

The modified Bessel function of the second kind is:

\[K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)}\]

Ordinary Bessel Functions

The Bessel function of the first kind of order n is defined as:

\[J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

The Bessel function of the second kind of order n is:

\[Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]
Application Areas

The exponentially scaled Bessel function is particularly important in numerical mathematics, signal processing, quantum physics, and all areas where large argument values can occur. It enables stable calculations even in extreme parameter ranges.


More complex functions

Absolute value (abs) • Angle • Conjugate • Division • Exponent • Logarithm to base 10 • Multiplication • Natural logarithm • Polarform • Power • Root • Reciprocal • Square root •
Cosh • Sinh • Tanh •
Acos • Asin • Atan • Cos • Sin • Tan •
Airy function • Derivative Airy function •
Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye •