Modified Bessel-K Function for Complex Numbers

Calculation of the modified Bessel function \(K_\nu(z)\) of the second kind with exponentially decaying behavior

Bessel-K Function Calculator

Modified Bessel Function \(K_\nu(z)\) of the Second Kind

The modified Bessel function of the second kind \(K_\nu(z)\) exhibits exponentially decaying behavior and is singular at the origin. It is a solution of the modified Bessel differential equation.

Complex Argument z = a + bi
+
i
Integer or rational order of the Bessel function
Calculation Result
\(K_\nu(z)\) =

Bessel-K Properties

Behavior

Decaying

Exponentially → 0

For large |z|
Kind

Second Kind

Type: \(K_\nu\)

Singular at z=0
Order

ν ∈ ℝ

Any real number

Integer or rational
Argument

z ∈ ℂ

Complex: a+bi

Real and imaginary part
Important Properties
  • Solution of the modified Bessel differential equation
  • Exponentially decaying behavior: \(K_\nu(z) \sim \sqrt{\frac{\pi}{2z}} e^{-z}\)
  • Singularity at the origin: \(K_\nu(0) = \infty\) (except special cases)
  • Symmetry relation: \(K_{-\nu}(z) = K_\nu(z)\)
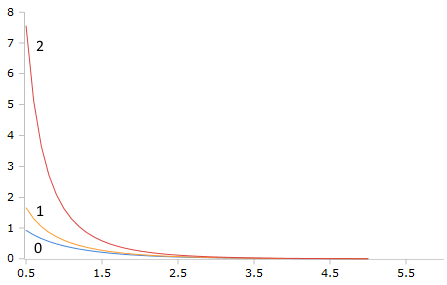
BesselK

Plot of the Bessel-K function with orders 0, 1 and 2

Definition of the Modified Bessel-K Function of the Second Kind

The modified Bessel function of the second kind \(K_\nu(z)\) is defined by:

Standard Definition
\[K_\nu(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_\nu(z)}{\sin(\nu \pi)}\]

Definition through the modified Bessel functions of the first kind \(I_\nu(z)\) and \(I_{-\nu}(z)\)

Modified Bessel ODE
\[z^2 \frac{d^2w}{dz^2} + z \frac{dw}{dz} - (z^2 + \nu^2)w = 0\]

Differential equation with solution \(w = K_\nu(z)\)

Integral Representation
\[K_\nu(z) = \int_0^\infty e^{-z\cosh t} \cosh(\nu t) \, dt\]

Valid for \(\text{Re}(z) > 0\)

Important Properties of the Bessel-K Function

Asymptotic Behavior
\[K_\nu(z) \sim \sqrt{\frac{\pi}{2z}} e^{-z}\]

Exponentially decaying for large |z|

Behavior at the Origin
\[K_0(z) \sim -\ln(z)\] \[K_\nu(z) \sim \frac{\Gamma(\nu)}{2}\left(\frac{2}{z}\right)^\nu \text{ for } \nu > 0\]

Singular at the origin for all ν

Symmetry Relations
\[K_{-\nu}(z) = K_\nu(z)\]

Symmetry with respect to order

Recurrence Relations
\[K_{\nu-1}(z) - K_{\nu+1}(z) = -\frac{2\nu}{z} K_\nu(z)\] \[K_{\nu-1}(z) + K_{\nu+1}(z) = -2 K_\nu'(z)\]

Relations between different orders

Applications of the Bessel-K Function

Heat Conduction
Cylindrical Bodies Steady States Temperature Distribution Diffusion Processes
Potential Theory
Electrostatics:
Cylindrical Charges
Shielding
Gravitation:
Mass Potentials
Cylindrical Distributions
Stochastics & Finance

Option Pricing Models

Brownian Motion

Variance Gamma Processes

Quantum Physics

Yukawa Potential

Scattering Theory

Shielding Effects

Tunneling Effects

Modified Bessel-K Functions - Detailed Description

Exponentially Decaying Behavior

The modified Bessel function of the second kind \(K_\nu(z)\) differs fundamentally from \(I_\nu(z)\) by its exponentially decaying behavior.

Characteristic Properties:
• Exponential decay for large |z|
• Singularity at the origin (z=0)
• Always positive for real positive z
• Bounded for large arguments

Historical Background

The modified Bessel functions were developed from the ordinary Bessel functions through the transformation \(z \to iz\). The K-functions are especially important for problems with exponentially decaying solutions.

Physical Interpretation

\(K_0(r)\) describes the steady-state temperature field of an infinitely long line heat source in an unbounded medium. The function decays exponentially with distance r.

Numerical Aspects

The K-functions are numerically well-behaved, as they decay exponentially for large arguments and exhibit no oscillations.

Numerical Properties:
• No overflow problems for large |z|
• Stable calculations possible
• Forward recurrence stable
• Singularity at origin requires caution

Calculation Methods

Various numerical methods are used depending on the argument range:

Small |z|: Series expansion around z=0
Moderate |z|: Integral representation
Large |z|: Asymptotic expansion \(\sim e^{-z}/\sqrt{z}\)
Complex z: Special algorithms required

Special Values

Some important limits:
\(\lim_{z \to 0^+} K_0(z) = +\infty\) (logarithmic singularity)
\(\lim_{z \to \infty} K_\nu(z) = 0\) (exponential decay)

Comparison: Bessel-K vs. Bessel-I

Modified Bessel-K Function (second kind)
Definition: \(K_\nu(z)\) via \(I_{\pm\nu}(z)\)
Behavior: Exponentially decaying
ODE: \(z^2w'' + zw' - (z^2+\nu^2)w = 0\)
Asymptotics: \(\sim \sqrt{\frac{\pi}{2z}} e^{-z}\)
Origin: Singular at z=0
Modified Bessel-I Function (first kind)
Definition: \(I_\nu(z) = i^{-\nu} J_\nu(iz)\)
Behavior: Exponentially growing
ODE: \(z^2w'' + zw' - (z^2+\nu^2)w = 0\)
Asymptotics: \(\sim \frac{e^z}{\sqrt{2\pi z}}\)
Origin: Finite at z=0
Application Guidelines
  • Heat conduction: K for cooling, heat dissipation
  • Diffusion: K for concentration decrease
  • Yukawa potential: K-function describes shielding
  • Unbounded domains: K for boundary behavior at infinity
  • Steady states: K for exponential decay
  • Mathematical finance: K in option pricing models

Bessel Functions - Complete Definitions and Relations

Ordinary Bessel Functions

The Bessel function of the first kind of order n is defined as:

\[J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

The Bessel function of the second kind (Neumann function) is:

\[Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]
Applications of J-Functions

Ordinary Bessel functions for oscillating phenomena with cylindrical symmetry: vibrations, electromagnetic waves, quantum mechanics.

Modified Bessel Functions

The modified Bessel function of the first kind is defined as:

\[I_{\nu}(z) = i^{-\nu} J_{\nu}(iz)\]

The modified Bessel function of the second kind is:

\[K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)}\]
Wronskian Determinant

For the modified Bessel functions:
\(W[I_\nu(z), K_\nu(z)] = I_\nu(z)K_\nu'(z) - I_\nu'(z)K_\nu(z) = -\frac{1}{z}\)

This shows that \(I_\nu\) and \(K_\nu\) are linearly independent solutions of the modified Bessel differential equation.


More complex functions

Absolute value (abs) • Angle • Conjugate • Division • Exponent • Logarithm to base 10 • Multiplication • Natural logarithm • Polarform • Power • Root • Reciprocal • Square root •
Cosh • Sinh • Tanh •
Acos • Asin • Atan • Cos • Sin • Tan •
Airy function • Derivative Airy function •
Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye •