Exponentially Scaled Bessel-Ke Function for Complex Numbers

Calculation of the exponentially scaled Bessel function \(K_e(z) = e^z K_\nu(z)\) of the second kind

Bessel-Ke Function Calculator

Exponentially Scaled Bessel Function \(K_e(z)\)

The exponentially scaled modified Bessel function \(K_e(z) = e^z K_\nu(z)\) prevents numerical underflows for large arguments by compensating the exponential decay of \(K_\nu(z)\).

Complex Argument z = a + bi
+
i
Integer or rational order of the Bessel function
Calculation Result
\(K_e(z)\) =

Bessel-Ke Properties

Scaling

Exponential

Factor: \(e^z\)

Prevents underflow
Original

Decaying

Type: \(K_\nu(z)\)

Exponentially → 0
Order

ν ∈ ℝ

Any real number

Integer or rational
Argument

z ∈ ℂ

Complex: a+bi

Real and imaginary part
Important Properties
  • Numerically stable calculation for large |z|
  • Compensates exponential decay of \(K_\nu(z)\)
  • Defined as: \(K_e(z) = e^z K_\nu(z)\)
  • Asymptotically: \(K_e(z) \sim \sqrt{\frac{\pi}{2z}}\) for |z| → ∞
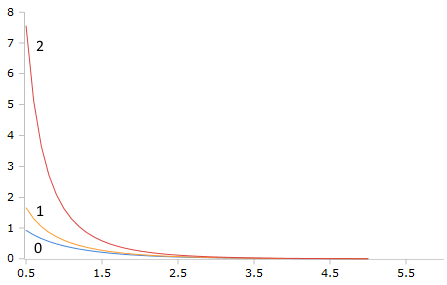
BesselK

Plot of the Bessel-K function (before exponential scaling)

Definition of the Exponentially Scaled Bessel-Ke Function

The exponentially scaled modified Bessel function of the second kind \(K_e(z)\) is defined as:

Scaled Definition
\[K_e(z) = e^z K_\nu(z) = e^z \cdot \frac{\pi}{2} \frac{I_{-\nu}(z) - I_\nu(z)}{\sin(\nu \pi)}\]

Exponentially scaled version to avoid numerical underflows in decaying functions

Numerical Stability
\[K_e(z) \sim \sqrt{\frac{\pi}{2z}} \text{ for } |z| \to \infty\]

Bounded for large |z|, prevents underflow

Relationship to Bessel-K
\[K_\nu(z) = e^{-z} K_e(z)\]

Back-transformation to the original function

Important Properties of the Scaled Bessel-Ke Function

Asymptotic Behavior
\[K_e(z) \sim \sqrt{\frac{\pi}{2z}}\]

Bounded behavior for large |z| (without exponential factor)

Numerical Advantages
\[\min K_e(z) > 0 \quad \text{for large } |z|\]

Avoids underflow despite exponential decay of \(K_\nu\)

Scaling Factor
\[s(z) = e^z = e^{\text{Re}(z)} \cdot e^{i\text{Im}(z)}\]

Exponential amplification factor compensates decay

Recurrence Relations
\[K_{e,\nu-1}(z) - K_{e,\nu+1}(z) = -\frac{2\nu}{z} K_{e,\nu}(z)\]

Scaled recurrence relations apply analogously

Applications of the Scaled Bessel-Ke Function

Numerical Analysis
Large arguments Underflow prevention Stable algorithms Precise calculation
Heat Conduction
Far-field:
Large distances
Steady states
Diffusion:
Long-term behavior
Decay processes
Quantum Physics

Yukawa potential

Screening

Far-field analysis

Financial Mathematics

Option prices

Variance-gamma

Long-term risk

Tail behavior

Exponentially Scaled Bessel-Ke Functions - Detailed Description

Numerical Stability with Decay

The exponentially scaled Bessel-Ke function \(K_e(z)\) was developed to solve the numerical problems of the modified Bessel function \(K_\nu(z)\) for large arguments, where the function decays exponentially to zero.

Problem Statement:
• \(K_\nu(z) \sim e^{-z}/\sqrt{z}\) for large |z|
• Numerical underflows for large |z|
• Loss of precision due to very small values
• Difficult calculation of ratios

Solution Approach

By the definition \(K_e(z) = e^z K_\nu(z)\), the exponentially decaying function is provided with an exponential amplification factor, so that the resulting function remains numerically manageable.

Advantages of Scaling

Without scaling: \(K_\nu(100) \approx 10^{-44}\) (underflow!)
With scaling: \(K_{e,\nu}(100) \approx 0.088\) (stable)

Mathematical Properties

The scaled function retains all important mathematical properties of the original decaying Bessel function, but is numerically more stable.

Preserved Properties:
• Recurrence relations remain valid
• Symmetry relations persist
• Singularity at origin preserved
• Asymptotic behavior known

Implementation

In numerical practice, the scaled version is used for large arguments and the result is back-transformed if needed:

\[K_\nu(z) = e^{-z} \cdot K_e(z)\]

Caution: Back-transformation can cause underflow again!

Computer Implementation

Modern libraries use the scaled version automatically for large arguments and handle the scaling transparently in the background.

Comparison: Scaled vs. Unscaled

Unscaled Bessel-K Function
Definition: \(K_\nu(z)\)
Behavior: Exponentially decaying
Problems: Underflow for large |z|
Numerics: Critical for |z| > 50
Scaled Bessel-Ke Function
Definition: \(K_e(z) = e^z K_\nu(z)\)
Behavior: Asymptotically constant
Advantages: No underflow problems
Range: All |z| (practically unlimited)
Practical Application Guidelines
  • Small |z| ≤ 10: Both versions usable
  • Medium |z| ≤ 50: Scaled version recommended
  • Large |z| > 50: Only use scaled version
  • Heat conduction: Always scaled version in far-field
  • Yukawa potential: Scaling for large distances
  • Financial mathematics: Transparent scaling

Bessel Functions - Complete Definitions and Scaling

Ordinary Bessel Functions

The Bessel function of the first kind of order n is defined as:

\[J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

The Bessel function of the second kind is:

\[Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]

Modified Bessel Functions

The modified Bessel function of the first kind is:

\[I_{\nu}(z) = i^{-\nu} J_{\nu}(iz)\]

The modified Bessel function of the second kind is:

\[K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)}\]

The exponentially scaled version is:

\[K_e(z) = e^z K_{\nu}(z)\]
Application Areas

The exponentially scaled Bessel-Ke function is particularly important for far-field analyses with exponentially decaying solutions, heat conduction over large distances, Yukawa potentials, and all areas where \(K_\nu(z)\) must be calculated for large arguments.


More complex functions

Absolute value (abs) • Angle • Conjugate • Division • Exponent • Logarithm to base 10 • Multiplication • Natural logarithm • Polarform • Power • Root • Reciprocal • Square root •
Cosh • Sinh • Tanh •
Acos • Asin • Atan • Cos • Sin • Tan •
Airy function • Derivative Airy function •
Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye •