Voltage divider
Online calculator for calculating the values on an unloaded voltage divider
The voltage divider is one of the most important basic circuits in electrical engineering. With this online calculator you can calculate all voltages and resistances in an unloaded voltage divider. The circuit consists of two resistors connected in series that divide an input voltage proportionally.
- Option 1: 2 voltage values + 1 resistance value
- Option 2: 1 voltage value + 2 resistance values
Functionality: In a voltage divider, the partial voltages behave like the corresponding resistances. This makes it possible to generate specific lower voltages from a higher voltage.
|
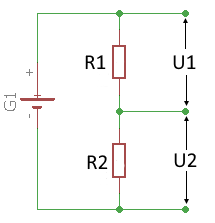
Circuit diagram: Unloaded voltage divider
Voltage divider formulas and theory
Basic principle
The voltage divider is a series circuit of two resistors through which an electrical voltage is divided. The ratio of the partial voltages corresponds to the ratio of the resistances.
1. Voltage divider formula
The most important formula for calculating the partial voltage U₂ across R₂ is:
\[U_2 = U_{total} \cdot \frac{R_2}{R_1 + R_2}\]
Correspondingly for the voltage U₁ across R₁:
\[U_1 = U_{total} \cdot \frac{R_1}{R_1 + R_2}\]
2. Alternative calculation via current
Alternatively, the partial voltage can be calculated via the current. First determine the total resistance:
\[R_{total} = R_1 + R_2\]
Then calculate the current according to Ohm's law:
\[I = \frac{U_{total}}{R_{total}}\]
The partial voltages then result in:
\[U_1 = R_1 \cdot I \quad \text{and} \quad U_2 = R_2 \cdot I\]
3. Resistance calculation
When voltages are known, the resistances can be calculated:
Calculate resistance R₁:
\[R_1 = \frac{U_1 \cdot R_2}{U_2} = \frac{U_1 \cdot R_2}{U_{total} - U_1}\]
Calculate resistance R₂:
\[R_2 = \frac{U_2 \cdot R_1}{U_1} = \frac{R_1 \cdot (U_{total} - U_1)}{U_1}\]
Practical calculation examples
Example 1: Calculate voltage U₂
Given: Utotal = 12V, R₁ = 3kΩ, R₂ = 6kΩ
Find: Voltage U₂
Calculation:
\[U_2 = 12V \cdot \frac{6k\Omega}{3k\Omega + 6k\Omega} = 12V \cdot \frac{6}{9} = 8V\]
Result: The output voltage U₂ is 8V
Example 2: Calculate resistance R₂
Given: Utotal = 9V, U₂ = 3V, R₁ = 1kΩ
Find: Resistance R₂
Calculation:
U₁ = Utotal - U₂ = 9V - 3V = 6V
\[R_2 = \frac{U_2 \cdot R_1}{U_1} = \frac{3V \cdot 1k\Omega}{6V} = 0.5k\Omega = 500\Omega\]
Result: The resistance R₂ is 500Ω
Example 3: Generate reference voltage
Task: Generate a reference voltage of 2V from 5V. R₁ = 1kΩ is given.
Find: Resistance R₂
Calculation:
From \(U_2 = U_{total} \cdot \frac{R_2}{R_1 + R_2}\) follows:
\[\frac{2V}{5V} = \frac{R_2}{1k\Omega + R_2}\]
\[0.4 = \frac{R_2}{1k\Omega + R_2}\]
Solving gives: R₂ = 667Ω (nearest standard value: 680Ω)
Practical applications
Common applications
- Reference voltages: Generation of stable reference voltages for analog circuits
- ADC interface: Voltage adaptation for analog-to-digital converters
- Sensor interfaces: Signal conditioning of sensor signals
- Bias circuits: Operating point adjustment in amplifiers
- Level converters: Adaptation between different logic levels
- Measurement circuits: Voltage reduction for measuring instruments
Design guidelines
- Consider loading: Loading changes the division ratio → see loaded voltage divider
- Current consumption: Voltage dividers consume current continuously
- Temperature drift: Resistance changes affect the output voltage
- Noise: Higher resistances generate more thermal noise
- Frequency response: Parasitic capacitances can interfere at high frequencies
Design recommendations
- Total resistance: 1kΩ - 100kΩ for typical applications
- Load resistance: Should be at least 10x larger than R₂
- Tolerances: Precision resistors (±1% or better) for accurate division
- Temperature coefficient: Use same TC values for both resistors
Difference to other circuits
| Circuit type | Characteristic | Application |
|---|---|---|
| Unloaded voltage divider | Constant division ratio | Reference voltages, measurement circuits |
| Loaded voltage divider | Division ratio changes with load | Signal sources with variable load |
| Voltage regulator | Constant output voltage | Power supplies |
Note: For applications with changing loads use the calculator for loaded voltage dividers.