Calculate Trapezoid Area
Calculator and formulas for calculating trapezoid area
Trapezoid Area Calculator
Trapezoid Area Calculation
The area A of a trapezoid is calculated from the parallel sides a and c and the height h. The formula is based on the arithmetic mean of the parallel sides.
Trapezoid with Area Marking
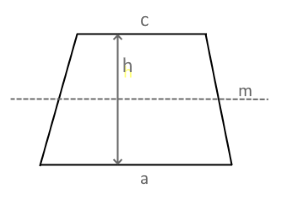
The diagram shows a trapezoid with parallel sides a and c and height h.
The area is calculated from the arithmetic mean of the parallel sides.
Area Calculation for Trapezoids
The area calculation for trapezoids is based on an elegant geometric relationship:
- Parallel sides: a and c are the two parallel sides
- Height h: Perpendicular distance between the parallel sides
- Arithmetic mean: (a+c)/2 gives the average width
- Rectangle analogy: Area = average width × height
- Universal formula: Works for all trapezoid shapes
- Limiting cases: When a=c, it becomes a rectangle
Derivation of the Trapezoid Area Formula
The geometric derivation explains why the formula works:
1. Duplication
- Trapezoid is duplicated
- Second trapezoid rotated 180°
- Both trapezoids joined together
- Parallelogram with double area is created
2. Rectangle Transformation
- Oblique sides are cut off
- Repositioned to form a rectangle
- Rectangle: length = (a+c), height = h
- Area = (a+c)×h, divided by 2
Alternative: Midline Method
An alternative approach uses the midline of the trapezoid:
Midline m
Arithmetic mean of the parallel sides
Simplified Formula
Area = Midline × Height
Practical Applications of Trapezoid Area Calculation
The area calculation of trapezoids is important in many fields:
Construction & Architecture
- Roof surfaces with trapezoidal shape
- Property and room areas
- Facade elements and windows
- Stairs and ramps
Engineering & Production
- Material requirement calculation
- Sheet metal cuts and profiles
- Channels and pipelines
- Mechanical engineering components
Agriculture & Environment
- Farmland and parcels
- Water surfaces and ponds
- Embankments and dams
- Nature reserves
Science & Research
- Numerical integration (trapezoidal rule)
- Statistics and data analysis
- Physical measurements
- Geological surveys
Formulas for Trapezoid Area Calculation
Main Formula: Trapezoid Area
Area from parallel sides a, c and height h
Midline m
Arithmetic mean of the parallel sides
Alternative Form
Area as midline times height
Special Case: Rectangle
With equal parallel sides it becomes a rectangle
Derivation via Rectangle
Geometric derivation through duplication
Step-by-Step Derivation
Rotate second trapezoid 180° and attach
Result: Parallelogram with double area
Cut off oblique sides and reposition
Result: Rectangle (a+c) × h
Divide rectangle area by 2
Since the rectangle is twice as large
\(A = \frac{(a+c) \cdot h}{2}\)
Universal trapezoid area formula
Visual Derivation of the Trapezoid Area Formula
Step 1: Duplication and Rotation
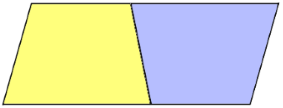
The trapezoid is duplicated and the second is rotated 180° and attached.
Step 2: Transform to Rectangle
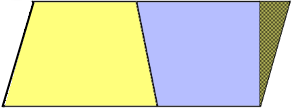
Oblique side is cut off...
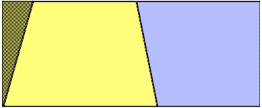
...and added to the other side.
Result of the Derivation
The resulting rectangle has length (a+c) and height h. Since it has double the area of the original trapezoid, the trapezoid area is: \[A_{Trapezoid} = \frac{A_{Rectangle}}{2} = \frac{(a+c) \cdot h}{2}\]
Calculation Example
Given
Find: Area A of the trapezoid
1. Calculate midline
Arithmetic mean of the parallel sides
2. Calculate area (Method 1)
Using the midline
3. Calculate area (Method 2 - Main Formula)
Direct application of the main formula
4. Verification through Derivation
\[A_{Rectangle} = (a + c) \cdot h = (3 + 5) \cdot 4 = 8 \cdot 4 = 32\]
Trapezoid area (half of rectangle):
\[A_{Trapezoid} = \frac{A_{Rectangle}}{2} = \frac{32}{2} = 16\]
All three methods lead to the same result
Trapezoid Area Calculation in Theory and Practice
The calculation of the area of a trapezoid is a fundamental concept in geometry that extends far beyond mathematical education. The elegant formula A = (a+c)·h/2 combines geometric intuition with practical applicability and forms the basis for numerous calculations in engineering, construction, and natural sciences.
Geometric Fundamentals
The trapezoid area formula is based on fundamental geometric principles:
- Parallelism: The two sides a and c are parallel to each other
- Height as distance: h is the perpendicular distance between the parallel sides
- Arithmetic mean: (a+c)/2 represents the "average width"
- Rectangle analogy: The trapezoid behaves area-wise like a rectangle with average width
- Universality: The formula applies to all trapezoid variants (isosceles, right-angled, general)
Mathematical Elegance of the Derivation
The geometric derivation of the formula shows the beauty of mathematical thinking:
Duplication Method
By rotating and joining two identical trapezoids, a parallelogram is created. This method illustrates the connection to the average width.
Rectangle Transformation
The transformation of the parallelogram to a rectangle shows that the trapezoid area is exactly half of a corresponding rectangle.
Symmetry Properties
The formula reflects the symmetry properties of the trapezoid and shows why the average width can be considered representative.
Limiting Case Considerations
When a=c the trapezoid becomes a rectangle (A=a·h), when c=0 a triangle (A=a·h/2) - the formula remains valid.
Practical Significance and Applications
Trapezoid area calculation finds application in numerous practical areas:
Civil Engineering
- Foundation calculation for trapezoidal floor plans
- Earthworks and embankment calculations
- Roof surfaces with complex geometry
- Bridge and tunnel cross-sections
Mechanical Engineering
- Material requirement determination for profiles
- Cross-sectional areas of components
- Flow cross-sections in channels
- Heat exchanger surfaces
Agriculture and Environment
- Area calculation for agricultural parcels
- Water surfaces and irrigation systems
- Nature reserves and biotopes
- Erosion protection and embankment security
Numerical Mathematics
- Trapezoidal rule for numerical integration
- Approximation of curve integrals
- Finite element methods
- Statistical area estimation
Modern Developments and Technologies
In the digitized world, trapezoid area calculation gains new significance:
- CAD Systems: Automated area calculation in complex 3D models
- GIS Applications: Geographic information systems for land surveying
- Drone Surveying: Precise area determination from aerial images
- BIM Technology: Building Information Modeling for intelligent building planning
- Augmented Reality: Real-time calculation of areas in AR applications
- Machine Learning: Automatic shape recognition and area estimation
Educational Aspects
Trapezoid area calculation is excellently suited as a teaching example:
Mathematical Concepts
Connects geometric visualization with algebraic formula formation and shows the utility of the arithmetic mean.
Problem-Solving Strategies
The derivation demonstrates creative problem-solving approaches and shows how complex shapes can be reduced to simpler ones.
Practical Relevance
Offers numerous connections to real applications and motivates further learning.
Visualization
The graphical derivation supports understanding and makes abstract concepts tangible.
Summary
Trapezoid area calculation is more than just a geometric formula - it is a tool that connects theory and practice. From elegant mathematical derivation through diverse technical applications to modern digital implementations, it shows the timeless relevance of fundamental geometric concepts. The formula A = (a+c)·h/2 exemplifies the beauty and utility of mathematical thinking in a technological world.
|
|