Calculate Tri-Equilateral Trapezoid
Calculator and formulas for trapezoids with three equal sides
Tri-Equilateral Trapezoid Calculator
Special trapezoid form
In a tri-equilateral trapezoid three sides are equal in length: the two legs and one of the parallel sides. The fourth side has a different length.
Tri-Equilateral Trapezoid
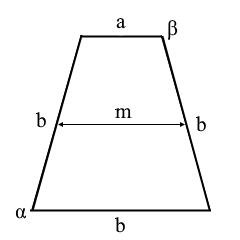

Tri-equilateral trapezoid with three equal sides b and one unequal side a.
The lower diagram shows the circumcircle.
The tri-equilateral trapezoid
A tri-equilateral trapezoid is a special form of trapezoid:
- Three equal sides: Both legs and one parallel side share the same length b
- One unequal side: The other parallel side has length a ≠ b
- Symmetry: Mirror-symmetric about the mid-perpendicular
- Special properties: Combines regularity with asymmetry
- Circumcircle: Has a unique circumcircle
- Use: Common in architecture and design
Symmetry and special properties
The tri-equilateral trapezoid exhibits unique geometric properties:
Axis of symmetry
- Mirror-symmetric about the mid-perpendicular
- Divides into two congruent right triangles
- Isosceles triangles at the ends
- Symmetric angle distribution
Circumcircle property
- All four vertices lie on a circle
- Unique circumradius determined
- Circle center on the symmetry axis
- Chord properties of the sides
Mathematical particularities
The geometric properties lead to special mathematical relations:
Formula simplification
- Simplified diagonal formula due to symmetry
- Height calculation via Pythagoras possible
- Direct relationship between a and b
- Perimeter as simple sum: P = a + 3b
Angle relations
- Base angles are complementary: α + β = 180°
- Symmetric angles on equal sides
- Arccos for angle computation
- Trigonometric simplifications possible
Practical applications
Tri-equilateral trapezoids are used in various fields:
Architecture & Construction
- Roof structures with special shapes
- Window and door frame design
- Bridge geometry and support structures
- Modern facade design
Design & Art
- Graphic design and logos
- Jewelry designs and ornaments
- Furniture design with geometric shapes
- Contemporary art and sculptures
Engineering & Mechanical Design
- Gear components and tooth profiles
- Optical elements and prisms
- Vehicle body parts
- Tooling design and fixtures
Science & Research
- Crystal structure analysis
- Molecular geometry studies
- Optics and wave theory
- Mathematical modeling
Formulas for the tri-equilateral trapezoid
Diagonal d
Simplified formula due to symmetry
Height h
From a right-angled subtriangle
Middle width m
Arithmetic mean of the parallel sides
Area A
Standard trapezoid area formula
Perimeter P
Simplified: one side a + three sides b
Angle α
with \(g = \frac{|a-b|}{2}\)
Via law of cosines in the subtriangle
Angle β
Complementary angle to α
Circumradius rc
Radius of the unique circumcircle
Calculation Example
Given
Find: All properties of the tri-equilateral trapezoid
1. Calculate diagonal
Simplified diagonal formula
2. Calculate height
From a right-angled subtriangle
3. Area
Standard trapezoid area formula
4. Perimeter
Simplified perimeter formula
5. Summary of all results
Complete characterization of the tri-equilateral trapezoid
The tri-equilateral trapezoid in theory and practice
The tri-equilateral trapezoid is a fascinating geometric shape that combines regularity with asymmetry. With three equal sides and one differing side it provides a unique balance between symmetry and variation. This special property makes it both mathematically interesting and practically valuable.
Geometric characteristics
The special properties of the tri-equilateral trapezoid arise from its unique structure:
- Three equal sides: Both legs and one parallel side have the same length b
- One differing side: The other parallel side has a different length a
- Axis symmetry: Symmetric about the mid-perpendicular of the parallel sides
- Existence of circumcircle: Has a unique circumcircle through all four vertices
- Special angle relations: Complementary base angles with trigonometric properties
Mathematical particularities
The mathematical properties lead to elegant formulas and relations:
Simplified calculations
Symmetry allows simplified formulas, especially for diagonal and perimeter. The equality of three sides reduces complexity significantly.
Trigonometric relations
Angle computation uses arccos, where the special side ratios lead to characteristic angles.
Circumcircle properties
As one of the few trapezoid types it has a circumcircle, leading to interesting geometric constructions.
Limit cases
For a = b it becomes a rhombus, for a = 0 it becomes an isosceles triangle - important special cases.
Constructive properties
The tri-equilateral trapezoid offers unique constructive advantages:
Stability and strength
- Even load distribution through three equal sides
- Reduced stress concentrations
- Symmetric force transfer
- High torsional stiffness
Manufacturing benefits
- Only two different side lengths required
- Simplified tooling production
- Reduced material variety
- Modular construction possible
Aesthetic qualities
- Balanced proportions
- Natural-looking asymmetry
- Harmonic form language
- Versatile design possibilities
Functional flexibility
- Adjustable proportions via the a/b ratio
- Scalable base form
- Combinable with other shapes
- Universally applicable
Modern applications and trends
In contemporary practice the tri-equilateral trapezoid gains relevance:
- Parametric design: CAD systems use the clear mathematical relations for automated construction
- Sustainable architecture: Optimized material use via standardized components
- Digital fabrication: 3D printing and CNC benefit from simplified geometries
- Biomimetics: Inspiration from natural forms with similar proportions
- Smart materials: Adaptive structures exploit special mechanical properties
- Modular construction: Prefabricated elements for efficient building
Summary
The tri-equilateral trapezoid represents a unique combination of mathematical elegance and practical applicability. Its special features — three equal sides, axis symmetry and the existence of a circumcircle — make it a valuable tool in geometry, construction and design. The simplified calculation formulas and versatile application possibilities demonstrate the potential of this often overlooked geometric shape.
|
|