Trapez Winkel berechnen
Rechner und Formeln zur Berechnung der Trapez-Winkel
Trapez Winkel Rechner
Trapez-Winkelberechnung
Die Winkel eines Trapezes werden aus der Höhe h und einer Seitenlänge (b oder d) berechnet. Wählen Sie aus, welche Winkel berechnet werden sollen.
Trapez mit Winkelmarkierung
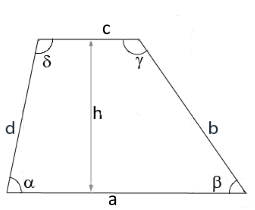
Das Diagramm zeigt ein Trapez mit den Winkeln α, β, γ, δ sowie der Höhe h und den Seiten b, d.
Die Winkelberechnung erfolgt über trigonometrische Funktionen.
Winkelbeziehungen im Trapez
Die Winkel eines Trapezes stehen in besonderen geometrischen Beziehungen zueinander:
- Supplementäre Winkel: α + δ = 180°, β + γ = 180°
- Winkelsumme: α + β + γ + δ = 360°
- Parallele Seiten: Erzeugen gleiche Nebenwinkel
- Trigonometrie: Winkel berechenbar über sin⁻¹(h/Seite)
- Spezialfall: Bei rechtwinkligem Trapez sind einige Winkel 90°
- Symmetrie: Bei gleichschenkligem Trapez: α = β, γ = δ
Formeln zur Trapez-Winkelberechnung
Winkel Alpha (α)
Berechnung über Höhe h und Seite d
Winkel Beta (β)
Berechnung über Höhe h und Seite b
Winkel Gamma (γ)
Supplementärwinkel zu β
Winkel Delta (δ)
Supplementärwinkel zu α
Allgemeine Winkelbeziehungen
\[\alpha + \beta + \gamma + \delta = 360°\] Wie bei jedem Viereck
\[\alpha + \delta = 180°\] \[\beta + \gamma = 180°\] Aufgrund der parallelen Seiten
Rechenbeispiel
Gegeben
Gesucht: Winkel α und δ
1. Winkel α berechnen
Arcussinus der Höhe durch Seite d
2. Winkel δ berechnen
Supplementärwinkel zu α
3. Kontrolle
Die Supplementärwinkel-Bedingung ist erfüllt
Praktische Anwendungen der Trapez-Winkelberechnung
Die Winkelberechnung bei Trapezen ist in vielen technischen Bereichen wichtig:
Bauwesen
- Dachneigungen und Sparrenwinkel
- Treppensteigungen und Rampen
- Böschungswinkel bei Erdarbeiten
- Fundamentneigungen
Maschinenbau
- Keilwinkel und Schrägungen
- Kanalprofil-Neigungen
- Führungsschienen-Winkel
- Werkzeugschneiden-Geometrie
Weitere Informationen zum Trapez
Ein Trapez ist ein Viereck mit vier Seiten. Da ein Trapez außerdem ein Paar paralleler Seiten hat, gibt es die zusätzliche Bedingung, dass das Winkelpaar entlang eines der Schenkel Ergänzungswinkel sind. Das heißt, ihre Summe muss 180 Grad (oder π Bogenmaß) betragen. Die Summe aller Winkel in einem Trapez beträgt 360 Grad (oder 2π Bogenmaß).
Die Kenntnis der Winkel eines Trapezes ist hilfreich, um seine Höhe zu bestimmen, die wiederum bei der Berechnung der Fläche des Trapezes hilft. Der Trapezwinkelrechner oben kann Ihnen bei der Bestimmung der Winkel helfen, wenn man die Höhe des Trapezes und die Länge eines Beins angibt.
Zur Berechnung der weiteren Parameter finden Sie auf den nächsten Seiten verschiedene Trapezrechner für unterschiedliche Anwendungsfälle.
|
|