Symmetrisches Trapez berechnen
Rechner und Formeln zum symmetrischen (gleichschenkligen) Trapez
Symmetrisches Trapez Rechner
Symmetrisches Trapez
Ein symmetrisches (gleichschenkliges) Trapez hat gleich lange Schenkel (b = d) und ist symmetrisch zur Mittelsenkrechten. Berechnung über Seiten und Höhe oder Seiten und Winkel möglich.
Symmetrisches Trapez
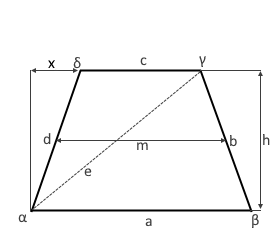
Das Diagramm zeigt ein symmetrisches Trapez mit gleich langen Schenkeln (b = d).
Die Symmetrieachse verläuft senkrecht durch die Mitte der parallelen Seiten.
Eigenschaften des symmetrischen Trapezes
Ein symmetrisches (gleichschenkliges) Trapez besitzt besondere geometrische Eigenschaften:
- Gleiche Schenkel: b = d (schräge Seiten sind gleich lang)
- Symmetrieachse: Senkrecht durch die Mitte der Parallelseiten
- Gleiche Basiswinkel: α = β und γ = δ
- Gleiche Diagonalen: Beide Diagonalen sind gleich lang
- Achsensymmetrie: Spiegelung an der Mittelsenkrechten
- Besondere Formeln: Vereinfachte Berechnungen möglich
Formeln für das symmetrische Trapez
Seitenlängen
Grundlegende Seitenberechnungen
Fläche und Umfang
Da b = d vereinfacht sich der Umfang
Winkel
Symmetrie: α = β und γ = δ
Diagonalen und Höhe
Beide Diagonalen sind gleich lang
Rechenbeispiel
Gegeben
Gesucht: Alle Parameter des symmetrischen Trapezes
1. Mittlere Breite und Fläche
Grundlegende Berechnungen
2. Schenkel über Überstand
Berechnung der gleichen Schenkel
3. Winkel berechnen
Symmetrische Winkelpaarung
4. Umfang und Diagonalen
Alle Eigenschaften der Symmetrie erfüllt
Anwendungen des symmetrischen Trapezes
Symmetrische Trapeze finden aufgrund ihrer besonderen Eigenschaften häufig Verwendung:
Architektur & Design
- Dachkonstruktionen mit gleichmäßiger Neigung
- Symmetrische Fenster und Türöffnungen
- Brückenbögen und Gewölbe
- Treppengeländer und Balustraden
Technik & Produktion
- Getriebezahnräder mit symmetrischen Profilen
- Keilriemenscheiben und Riementriebe
- Strömungskanäle mit optimaler Verteilung
- Werkzeugschneiden und Fräsprofile
Das symmetrische Trapez in der Geometrie
Zum Berechnen des symmetrischen Trapezes (auch gleichschenkliges Trapez genannt) geben Sie entweder die Seiten a und c sowie die Höhe oder die Seiten a und d sowie den Winkel Alpha ein. Das symmetrische Trapez ist ein spezieller Fall des allgemeinen Trapezes mit besonderen Symmetrieeigenschaften.
Die Gleichheit der Schenkel (b = d) führt zu vereinfachten Berechnungsformeln und besonderen geometrischen Eigenschaften wie gleichen Diagonalen und symmetrischen Winkeln. Diese Eigenschaften machen das symmetrische Trapez zu einer wichtigen geometrischen Form in Architektur, Technik und Design.
Für weitere Trapez-Berechnungen stehen Ihnen verschiedene spezialisierte Rechner zur Verfügung, die auf die jeweiligen Anwendungsfälle optimiert sind.
|
|