Trapez Diagonale e mit Winkel berechnen
Rechner und Formeln zur Trapez Diagonalen e über Seitenlängen und Winkel
Trapez Diagonale e (Winkel-Methode)
Winkel-basierte Berechnung
Bei bekannten Seitenlängen a und b und einem Winkel β kann die Diagonale e direkt mit dem Cosinussatz berechnet werden, ohne die Höhe zu benötigen.
Trapez mit Winkel β
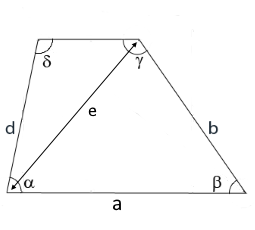
Das Diagramm zeigt ein Trapez mit den Seiten a und b und dem Winkel β.
Die Diagonale e wird über den Cosinussatz berechnet.
Winkel-basierte Diagonalen-Berechnung
Die winkel-basierte Methode zur Berechnung der Trapez-Diagonale bietet Vorteile:
- Direkter Ansatz: Keine Höhenberechnung erforderlich
- Cosinussatz: Bewährte trigonometrische Methode
- Flexibilität: Funktioniert bei verschiedenen Trapez-Formen
- Genauigkeit: Präzise Ergebnisse bei bekannten Winkeln
- Anwendung: Besonders nützlich in der Vermessung
- Ergänzung: Alternative zur höhen-basierten Berechnung
Der Winkel β im Trapez
Der Winkel β spielt eine zentrale Rolle in der Berechnung:
Definition
- Winkel zwischen den Seiten a und b
- Gemessen in Grad (°) oder Radiant
- Typischerweise zwischen 0° und 180°
- Bestimmt die Form des Trapezes
Einfluss auf Diagonale
- Cosinus des Winkels bestimmt die Länge
- Bei 90° entspricht es dem Pythagoras
- Spitze Winkel ergeben längere Diagonalen
- Stumpfe Winkel verkürzen die Diagonale
Der Cosinussatz im Trapez
Der Cosinussatz ermöglicht die direkte Berechnung der Diagonale:
Formel
Verallgemeinerung des Pythagoras
Anwendung
- Gültig für alle Dreiecke und Trapez-Teile
- Reduziert sich bei β=90° zum Pythagoras
- Berücksichtigt die Winkel-Geometrie
- Direkter Weg ohne Zwischenschritte
Berechnungsmethoden im Vergleich
Es gibt verschiedene Ansätze zur Berechnung der Trapez-Diagonale:
Mit Winkel
Cosinussatz direkt anwenden
Mit Höhe
Pythagoras in Teildreieck
Koordinaten
Analytische Geometrie
Formeln zur winkel-basierten Diagonalen-Berechnung
Hauptformel: Cosinussatz
Diagonale aus zwei Seiten und dem eingeschlossenen Winkel
Winkel in Radiant
Umrechnung von Grad in Radiant
Spezialfall β = 90°
Reduziert sich zum Pythagoras
Alternative Schreibweise
Ohne Wurzel für Zwischenrechnungen
Winkel zwischen anderen Seiten
Bei bekannten Seiten c, d und Winkel δ
Schritt-für-Schritt Berechnung
Falls nötig, Grad in Radiant umwandeln
Viele Rechner akzeptieren beide Einheiten
\(\cos(\beta)\) des gegebenen Winkels
Trigonometrische Funktion anwenden
\(e^2 = a^2 + b^2 - 2ab\cos(\beta)\)
Werte in die Cosinussatz-Formel
\(e = \sqrt{e^2}\)
Quadratwurzel für das Endergebnis
Wichtige Winkelwerte
- cos(0°) = 1: Maximaler Cosinus-Wert
- cos(60°) = 0.5: Häufig verwendeter Wert
- cos(90°) = 0: Rechter Winkel
- cos(120°) = -0.5: Stumpfer Winkel
- cos(180°) = -1: Minimaler Cosinus-Wert
- cos(30°) ≈ 0.866: Häufiger Referenzwert
- cos(45°) ≈ 0.707: Halber rechter Winkel
- cos(135°) ≈ -0.707: Stumpfer Standardwinkel
Rechenbeispiel
Gegeben
Gesucht: Diagonale e
1. Cosinus berechnen
Bekannter trigonometrischer Wert
2. Werte einsetzen
Cosinussatz anwenden
3. Endergebnis
Die Diagonale e hat eine Länge von etwa 5.29 Einheiten
4. Verifikation und Plausibilität
Plausibilitätsprüfung:
• Die Diagonale (5.29) liegt zwischen den Seitenlängen 4 und 6 ✓
• Bei 60° ist der Cosinus positiv (0.5), was eine moderate Verkürzung bewirkt ✓
• Ohne Winkel-Term wäre √(36+16) = √52 ≈ 7.21, mit Winkel kleiner ✓
Alternative Berechnung: Bei β=90° wäre e = √(36+16) = √52 ≈ 7.21
Da 60° < 90°, ist cos(60°) > 0, somit e < 7.21 ✓
Winkel-basierte Trapez-Diagonalen in Theorie und Praxis
Die winkel-basierte Berechnung der Trapez-Diagonale erweitert die geometrischen Möglichkeiten erheblich. Während die höhen-basierte Methode rechtwinklige Teilung nutzt, ermöglicht der Cosinussatz die direkte Berechnung aus Seitenlängen und Winkeln - ein Ansatz, der in der Vermessung und im Maschinenbau besonders wertvoll ist.
Der Cosinussatz - Fundamentale Erweiterung
Der Cosinussatz ist eine der wichtigsten Verallgemeinerungen des Pythagoras:
- Allgemeine Gültigkeit: Funktioniert für alle Dreiecke, nicht nur rechtwinklige
- Winkel-Integration: Berücksichtigt explizit die Winkel-Geometrie
- Pythagoras als Spezialfall: Bei 90° reduziert sich die Formel zum klassischen Pythagoras
- Vielseitigkeit: Ermöglicht Berechnungen mit verschiedenen Parametertypen
- Praktische Relevanz: Direkt anwendbar ohne Zwischenschritte
Winkel-Geometrie im Trapez
Winkel spielen in der Trapez-Geometrie eine fundamentale Rolle:
Innenwinkel-Eigenschaften
Die Summe aller Innenwinkel beträgt 360°. Gegenüberliegende Winkel an parallelen Seiten sind supplementär (ergänzen sich zu 180°).
Symmetrie-Beziehungen
Bei gleichschenkligen Trapezen sind die Basiswinkel paarweise gleich, was die Berechnung vereinfacht.
Praktische Messbarkeit
Winkel sind oft einfacher zu messen als Höhen, besonders in der Vermessung und bei unzugänglichen Objekten.
Konstruktive Bedeutung
In der Konstruktion werden Winkel oft als primäre Parameter vorgegeben, aus denen andere Größen abgeleitet werden.
Praktische Anwendungen der Winkel-Methode
Die winkel-basierte Diagonalen-Berechnung findet in vielen Bereichen Anwendung:
Vermessung und Kartografie
- Triangulation: Entfernungsbestimmung über Winkel
- Topografische Aufnahmen: Geländevermessung
- GPS-basierte Messungen: Satellitengeometrie
- Katastervermessung: Grundstücksgrenzen
Bauingenieurswesen
- Dachkonstruktionen: Sparrenberechnung
- Brückenbau: Fachwerkelemente
- Stahlbau: Verbindungsdiagonalen
- Betonbau: Schalungsgeometrie
Maschinenbau
- Getriebetechnik: Hebelgeometrie
- Robotik: Gelenkkinematik
- Fahrzeugtechnik: Aufhängungsgeometrie
- Werkzeugmaschinen: Führungsberechnung
Navigation und Orientierung
- Luftfahrt: Flugrouten-Berechnung
- Schifffahrt: Kursbestimmung
- Militär: Zielerfassung und Peilung
- Astronomie: Stern-Positionsbestimmung
Trigonometrische Grundlagen
Die Anwendung des Cosinussatzes erfordert solides Verständnis der Trigonometrie:
Cosinus-Funktion
Der Cosinus beschreibt das Verhältnis der Ankathete zur Hypotenuse. Bei stumpfen Winkeln (> 90°) wird er negativ, was mathematisch korrekt berücksichtigt wird.
Winkel-Einheiten
Grad (360° = Vollkreis) und Radiant (2π = Vollkreis) sind die gebräuchlichen Einheiten. Die meisten Rechner können zwischen beiden umschalten.
Genauigkeit und Präzision
Die Genauigkeit der Winkelangabe bestimmt die Präzision des Ergebnisses. Kleine Winkelfehler können große Auswirkungen auf die berechnete Diagonale haben.
Periodizität
Trigonometrische Funktionen sind periodisch. Bei Trapez-Berechnungen sind normalerweise Winkel zwischen 0° und 180° relevant.
Vergleich der Berechnungsmethoden
Verschiedene Methoden haben unterschiedliche Vor- und Nachteile:
Winkel-Methode (Cosinussatz)
Vorteile:
- Direkte Berechnung ohne Zwischenschritte
- Winkel oft leichter messbar als Höhen
- Funktioniert bei allen Trapez-Formen
- Mathematisch elegant und präzise
Nachteile:
- Erfordert trigonometrische Kenntnisse
- Winkelmessung kann fehleranfällig sein
- Rechner-abhängig für komplexe Berechnungen
Höhen-Methode (Pythagoras)
Vorteile:
- Anschaulich und geometrisch verständlich
- Nutzt vertraute Pythagoras-Beziehungen
- Höhen oft direkt messbar
- Weniger trigonometrische Kenntnisse nötig
Nachteile:
- Mehrere Berechnungsschritte erforderlich
- Höhenmessung nicht immer möglich
- Projektionsberechnung als Zwischenschritt
Historische Entwicklung
Die Entwicklung winkel-basierter Berechnungen hat eine lange Geschichte:
- Antike Trigonometrie: Erste systematische Winkel-Berechnungen durch griechische und islamische Mathematiker
- Cosinussatz: Verallgemeinerung des Pythagoras, vollständig entwickelt im Mittelalter
- Vermessungswesen: Praktische Anwendung in der Navigation und Kartografie seit der Renaissance
- Industrielle Revolution: Maschinenbau und Konstruktion als neue Anwendungsfelder
- Moderne Zeit: Computergestützte Berechnungen und GPS-Technologie
- Digitale Ära: Automatisierte Berechnungen in CAD und Simulation
Erweiterte Anwendungen
Moderne Anwendungen gehen weit über einfache Trapez-Berechnungen hinaus:
- 3D-Modellierung: Räumliche Trapez-Strukturen in CAD-Systemen
- Finite-Elemente-Analyse: Trapezoidale Elemente in der Strukturberechnung
- Computergrafik: Polygon-Rendering und geometrische Transformationen
- Robotik: Inverse Kinematik für Gelenkroboter
- Architektur: Parametrisches Design und geometrische Optimierung
- Physikalische Simulation: Kollisionserkennung und Bewegungsberechnung
Zusammenfassung
Die winkel-basierte Berechnung der Trapez-Diagonale mit dem Cosinussatz stellt eine elegante und praktische Alternative zur höhen-basierten Methode dar. Sie verbindet mathematische Eleganz mit praktischer Anwendbarkeit und ist besonders wertvoll, wenn Winkel leichter zu bestimmen sind als Höhen. Die Methode bildet eine Brücke zwischen grundlegender Geometrie und fortgeschrittener Trigonometrie und demonstriert die Vielseitigkeit mathematischer Ansätze in der Problemlösung.
Alternative Berechnungsmethoden
Neben der winkel-basierten Methode existieren weitere Ansätze zur Berechnung der Trapez-Diagonale:
Höhen-basierte Berechnung
Wenn die Höhe h bekannt ist, kann die Diagonale über rechtwinklige Teildreiecke berechnet werden:
Schritt 1: Projektion berechnen
Horizontale Projektion der schrägen Seite
Schritt 2: Diagonale bestimmen
Pythagoras im rechtwinkligen Teildreieck
Koordinaten-basierte Berechnung
Platzierung des Trapezes in einem Koordinatensystem ermöglicht analytische Berechnung:
Distanzformel anwenden
Euklidische Distanz zwischen den Eckpunkten der Diagonale
Vergleich der Methoden
Winkel-Methode
Eingabe: Seiten a, b + Winkel β
Formel: Cosinussatz
Vorteil: Direkt, keine Höhe nötig
Nachteil: Trigonometrie erforderlich
Höhen-Methode
Eingabe: Seiten a, b + Höhe h
Formel: Pythagoras
Vorteil: Anschaulich, vertraut
Nachteil: Mehrere Schritte
Koordinaten-Methode
Eingabe: Eckpunkt-Koordinaten
Formel: Distanzformel
Vorteil: Universell anwendbar
Nachteil: Koordinaten-Setup nötig
|
|