Trapez Diagonale e berechnen
Rechner und Formeln zur Trapez Diagonalen e über Seitenlängen und Höhe
Trapez Diagonale e Rechner
Trapez Diagonale
Ein Trapez hat zwei parallele Seiten. Die Diagonale e verbindet zwei nicht benachbarte Eckpunkte und kann aus den Seitenlängen und der Höhe berechnet werden.
Trapez mit Diagonale e
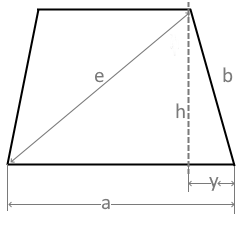
Das Diagramm zeigt ein Trapez mit den Seiten a und b, der Höhe h und der Diagonale e.
Die Diagonale e verbindet zwei nicht benachbarte Eckpunkte.
Was ist ein Trapez?
Ein Trapez ist ein Viereck mit besonderen Eigenschaften:
- Zwei parallele Seiten: Die Grundflächen sind parallel zueinander
- Verschiedene Längen: Die parallelen Seiten haben meist unterschiedliche Längen
- Schräge Seiten: Die nicht-parallelen Seiten verbinden die Grundflächen
- Höhe: Der senkrechte Abstand zwischen den parallelen Seiten
- Diagonalen: Verbindungslinien zwischen nicht benachbarten Eckpunkten
- Anwendung: Architektur, Ingeneurswesen, Dachkonstruktionen
Die Diagonale e im Trapez
Die Diagonale e ist eine wichtige Größe in der Trapez-Geometrie:
Definition
- Verbindet zwei nicht benachbarte Eckpunkte
- Teilt das Trapez in zwei Dreiecke
- Eine von zwei möglichen Diagonalen
- Länge abhängig von Seitenlängen und Höhe
Berechnung
- Pythagoras in rechtwinkligem Teildreieck
- Koordinatengeometrie möglich
- Trigonometrische Beziehungen
- Vektorrechnung als Alternative
Praktische Anwendungen
Trapez-Diagonalen sind in vielen praktischen Bereichen wichtig:
Bauwesen & Architektur
- Dachkonstruktionen und Giebel
- Brückenbau und Tragwerke
- Verstrebungen und Aussteifungen
- Trapezoide Fenster und Türen
Technik & Design
- Maschinenbau: Keilverbindungen
- Fahrzeugbau: Karosserieteile
- Möbeldesign: geometrische Formen
- Gartengestaltung: Beete und Wege
Berechnungsmethoden
Die Diagonale e kann auf verschiedene Weise berechnet werden:
Pythagoras
Rechtwinkliges Teildreieck nutzen
Koordinaten
Kartesisches Koordinatensystem
Trigonometrie
Winkel und trigonometrische Funktionen
Formeln zur Berechnung der Diagonale e
Hauptformel mit Seiten a, b und Höhe h
Dabei ist: \(y = \sqrt{b^2 - h^2}\)
Berechnung von y
Horizontaler Abstand der schrägen Seite
Alternative mit Seiten c, d
Mit \(x = \sqrt{d^2 - h^2}\)
Koordinaten-Methode
Euklidische Distanz zwischen Eckpunkten
Mit Winkel β
Cosinussatz im Trapez-Teildreieck
Schritt-für-Schritt Berechnung
\(y = \sqrt{b^2 - h^2}\)
Horizontalprojektion der Seite b
\(e = \sqrt{(a-y)^2 + h^2}\)
Pythagoras im rechtwinkligen Dreieck
Bezeichnungen im Trapez
- a: Parallele Seite (oft die obere/kürzere)
- b: Schräge Seite des Trapezes
- c: Untere parallele Seite (oft länger)
- d: Andere schräge Seite
- h: Höhe (Abstand paralleler Seiten)
- e: Erste Diagonale
- f: Zweite Diagonale
- y, x: Horizontalprojektionen der schrägen Seiten
Rechenbeispiel
Gegeben
Gesucht: Diagonale e
1. Berechnung von y
Horizontale Projektion der schrägen Seite b
2. Berechnung der Diagonale e
Pythagoras im rechtwinkligen Teildreieck
3. Ergebnis
Die Diagonale e hat eine Länge von etwa 5.66 Einheiten
4. Verifikation
Kontrolle durch Koordinatengeometrie:
Eckpunkte: A(0,0), B(7,0), C(3,4), D(0,4)
Diagonale AC: \(\sqrt{(7-0)^2 + (0-4)^2} = \sqrt{49+16} = \sqrt{65} \approx 8.06\)
Diagonale BD: \(\sqrt{(3-0)^2 + (4-0)^2} = \sqrt{9+16} = \sqrt{25} = 5\)
Hinweis: Je nach Orientierung des Trapezes ergeben sich verschiedene Diagonalenlängen.
Das Trapez und seine Diagonalen in Mathematik und Praxis
Das Trapez ist ein faszinierendes geometrisches Objekt, das durch seine zwei parallelen Seiten charakterisiert ist. Die Diagonalen eines Trapezes spielen eine wichtige Rolle in der Geometrie und haben praktische Bedeutung in Architektur, Ingeneurswesen und Design.
Definition und Grundeigenschaften des Trapezes
Ein Trapez ist ein Viereck mit besonderen Eigenschaften:
- Zwei parallele Seiten: Die Grundflächen (Basen) sind parallel zueinander
- Zwei nicht-parallele Seiten: Die Schenkel verbinden die parallelen Seiten
- Höhe: Der senkrechte Abstand zwischen den parallelen Seiten
- Zwei Diagonalen: Verbindungslinien zwischen nicht benachbarten Eckpunkten
- Verschiedene Formen: Gleichschenklig, rechtwinklig oder allgemein
Die Diagonalen - Geometrische Bedeutung
Die Diagonalen eines Trapezes haben besondere geometrische Eigenschaften:
Strukturelle Eigenschaften
Diagonalen teilen das Trapez in vier Dreiecke, wobei gegenüberliegende Dreiecke ähnlich sind.
Schnittpunkt-Verhalten
Die Diagonalen schneiden sich im Inneren des Trapezes und teilen sich in charakteristischen Verhältnissen.
Längenbeziehungen
Die Längen der Diagonalen stehen in direkter Beziehung zu den Seitenlängen und der Höhe des Trapezes.
Symmetrie-Eigenschaften
Bei gleichschenkligen Trapezen sind beide Diagonalen gleich lang, bei allgemeinen Trapezen meist unterschiedlich.
Praktische Anwendungen
Trapez-Diagonalen finden in vielen praktischen Bereichen Anwendung:
Bauwesen und Konstruktion
- Dachkonstruktionen: Sparren und Verstrebungen
- Brückenbau: Fachwerkkonstruktionen
- Stahlbau: Aussteifungsdiagonalen
- Holzbau: Rahmenverbindungen
Maschinenbau
- Getriebetechnik: Keilverbindungen
- Fahrzeugbau: Chassisversteifungen
- Fördertechnik: Schüttgutbehälter
- Werkzeugmaschinen: Führungsschienen
Design und Architektur
- Fenster und Türen: Trapezoidale Öffnungen
- Möbeldesign: Moderne geometrische Formen
- Landschaftsarchitektur: Beete und Wegeführung
- Innenarchitektur: Raumaufteilung
Technik und Elektronik
- Optik: Prismengeometrie
- Elektronik: Leiterplattenformen
- Solartechnik: Panelausrichtung
- Antennentechnik: Richtstrahlgeometrie
Berechnungsmethoden im Detail
Die Berechnung der Trapez-Diagonale kann auf verschiedene Weise erfolgen:
Pythagoras-Methode
Die klassische Methode nutzt rechtwinklige Teildreiecke. Durch Projektion der schrägen Seiten entstehen rechtwinklige Dreiecke, in denen der Pythagoras angewendet werden kann.
Koordinatengeometrie
Platzierung des Trapezes in einem Koordinatensystem ermöglicht die Berechnung über die Distanzformel zwischen den Eckpunkten.
Trigonometrische Methoden
Mit bekannten Winkeln kann die Diagonale über Sinus-, Cosinus- oder Tangensfunktionen berechnet werden.
Vektorrechnung
Moderne Methode mit Vektoren ermöglicht elegante Berechnungen und ist besonders in 3D-Anwendungen vorteilhaft.
Mathematische Beziehungen
Trapez-Diagonalen folgen interessanten mathematischen Gesetzmäßigkeiten:
- Diagonalensatz: In einem Trapez mit parallelen Seiten a und c schneiden sich die Diagonalen so, dass sie ähnliche Dreiecke bilden
- Längenverhältnisse: Die Verhältnisse der Diagonalabschnitte entsprechen den Verhältnissen der parallelen Seiten
- Flächenbeziehungen: Die Diagonalen teilen das Trapez in vier Dreiecke mit besonderen Flächenverhältnissen
- Mittellinie: Die Mittellinie verbindet die Mittelpunkte der nicht-parallelen Seiten und ist parallel zu den Grundseiten
- Symmetrie-Eigenschaften: Bei gleichschenkligen Trapezen gelten zusätzliche Symmetriebeziehungen
Spezielle Trapez-Arten
Gleichschenkliges Trapez
Beide nicht-parallelen Seiten sind gleich lang. Die Diagonalen haben gleiche Länge und das Trapez ist achsensymmetrisch.
Rechtwinkliges Trapez
Eine der nicht-parallelen Seiten steht senkrecht zu den parallelen Seiten. Vereinfacht die Berechnung erheblich.
Schiefes Trapez
Allgemeine Form ohne besondere Symmetrien. Die Diagonalen haben meist unterschiedliche Längen.
Parallelogramm
Spezialfall mit zwei Paaren paralleler Seiten. Beide Diagonalen schneiden sich in ihren Mittelpunkten.
Historische und kulturelle Bedeutung
Das Trapez hat eine reiche Geschichte in verschiedenen Kulturen:
- Antike Geometrie: Bereits von den Babyloniern für Flächenberechnungen verwendet
- Ägyptische Mathematik: Pyramidenstümpfe als dreidimensionale Trapez-Anwendungen
- Griechische Geometrie: Systematische Untersuchung durch Euklid und andere
- Römische Ingenieurskunst: Anwendung in Aquädukten und Architektur
- Mittelalterliche Baukunst: Gotische Bögen und Fensterformen
- Renaissance: Perspektive und räumliche Darstellung
- Moderne Zeit: Ingenieursanwendungen und Computergrafik
Verwandte geometrische Konzepte
Das Trapez steht in Beziehung zu anderen geometrischen Formen:
- Dreiecke: Trapeze können als zusammengesetzte Dreiecke betrachtet werden
- Parallelogramme: Spezialfälle von Trapezen mit zwei Paaren paralleler Seiten
- Vierecke allgemein: Trapeze als spezielle Klasse von Vierecken
- Kreissektoren: Verwandtschaft in der Flächenberechnung
- Polygone: Trapeze als Bausteine komplexerer Polygone
Zusammenfassung
Die Diagonale e eines Trapezes ist mehr als nur eine geometrische Größe. Sie verbindet mathematische Theorie mit praktischen Anwendungen und zeigt, wie einfache geometrische Konzepte in komplexen technischen und architektonischen Lösungen zum Einsatz kommen. Die verschiedenen Berechnungsmethoden demonstrieren die Vielseitigkeit der Mathematik und ihre Anwendbarkeit in unterschiedlichen Kontexten.
|
|