Dreigleichseitiges Trapez berechnen
Rechner und Formeln für Trapeze mit drei gleichen Seiten
Dreigleichseitiges Trapez Rechner
Besondere Trapez-Form
Bei einem dreigleichseitigen Trapez sind drei Seiten gleich lang: die beiden Schenkel und eine der parallelen Seiten. Die vierte Seite hat eine andere Länge.
Dreigleichseitiges Trapez
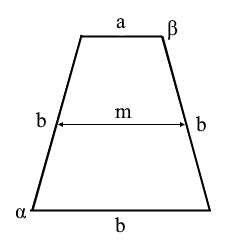

Dreigleichseitiges Trapez mit drei gleichen Seiten b und einer ungleichen Seite a.
Das untere Diagramm zeigt den Umkreis.
Das dreigleichseitige Trapez
Ein dreigleichseitiges Trapez ist eine besondere Form des Trapezes:
- Drei gleiche Seiten: Beide Schenkel und eine parallele Seite haben dieselbe Länge b
- Eine ungleiche Seite: Die andere parallele Seite hat die Länge a ≠ b
- Symmetrie: Spiegelsymmetrisch zur Mittelsenkrechten
- Besondere Eigenschaften: Kombiniert Regelmäßigkeit mit Asymmetrie
- Umkreis: Besitzt einen eindeutigen Umkreis
- Anwendung: Häufig in Architektur und Design verwendet
Symmetrie und besondere Eigenschaften
Das dreigleichseitige Trapez zeigt einzigartige geometrische Eigenschaften:
Symmetrieachse
- Spiegelsymmetrisch zur Mittelsenkrechten
- Teilung in zwei kongruente rechtwinklige Dreiecke
- Gleichschenklige Dreiecke an den Enden
- Symmetrische Winkelverteilung
Umkreis-Eigenschaft
- Alle vier Eckpunkte liegen auf einem Kreis
- Eindeutig bestimmter Umkreisradius
- Kreismittelpunkt auf der Symmetrieachse
- Sehnen-Eigenschaft der Seiten
Mathematische Besonderheiten
Die geometrischen Eigenschaften führen zu besonderen mathematischen Beziehungen:
Formelvereinfachung
- Vereinfachte Diagonalenformel durch Symmetrie
- Höhenberechnung über Pythagoras möglich
- Direkter Zusammenhang zwischen a und b
- Umfang als einfache Summe: P = a + 3b
Winkelbeziehungen
- Basiswinkel sind komplementär: α + β = 180°
- Symmetrische Winkel an den gleichen Seiten
- Arccos-Funktion für Winkelberechnung
- Trigonometrische Vereinfachungen möglich
Praktische Anwendungen
Dreigleichseitige Trapeze finden in verschiedenen Bereichen Anwendung:
Architektur & Bauwesen
- Dachkonstruktionen mit besonderen Formen
- Fenster- und Türrahmen-Design
- Brückengeometrie und Stützstrukturen
- Moderne Fassadengestaltung
Design & Kunst
- Grafische Gestaltung und Logos
- Schmuck-Design und Ornamente
- Möbeldesign mit geometrischen Formen
- Moderne Kunst und Skulpturen
Technik & Maschinenbau
- Getriebe-Komponenten und Zahnräder
- Optische Elemente und Prismen
- Fahrzeug-Karosserieteile
- Werkzeug-Design und Halterungen
Wissenschaft & Forschung
- Kristallstruktur-Analyse
- Molekulare Geometrie-Studien
- Optik und Wellenlehre
- Mathematische Modellierung
Formeln für das dreigleichseitige Trapez
Diagonale d
Vereinfachte Formel durch Symmetrie
Höhe h
Aus rechtwinkligem Teildreieck
Mittlere Breite m
Arithmetisches Mittel der parallelen Seiten
Flächeninhalt A
Standard Trapez-Flächenformel
Umfang P
Vereinfacht: eine Seite a + drei Seiten b
Winkel α
mit \(g = \frac{|a-b|}{2}\)
Über Cosinussatz im Teildreieck
Winkel β
Komplementärwinkel zu α
Umkreisradius rc
Radius des eindeutigen Umkreises
Rechenbeispiel
Gegeben
Gesucht: Alle Eigenschaften des dreigleichseitigen Trapezes
1. Diagonale berechnen
Vereinfachte Diagonalenformel
2. Höhe berechnen
Aus rechtwinkligem Teildreieck
3. Flächeninhalt
Standard Trapez-Flächenformel
4. Umfang
Vereinfachte Umfangsformel
5. Zusammenfassung aller Ergebnisse
Vollständige Charakterisierung des dreigleichseitigen Trapezes
Das dreigleichseitige Trapez in Theorie und Praxis
Das dreigleichseitige Trapez ist eine faszinierende geometrische Form, die Regelmäßigkeit mit Asymmetrie verbindet. Mit drei gleichen Seiten und einer abweichenden Seite stellt es eine einzigartige Balance zwischen Symmetrie und Variation dar. Diese besondere Eigenschaft macht es sowohl mathematisch interessant als auch praktisch wertvoll.
Geometrische Charakteristika
Die besonderen Eigenschaften des dreigleichseitigen Trapezes resultieren aus seiner einzigartigen Struktur:
- Drei gleiche Seiten: Beide Schenkel und eine Parallelseite haben dieselbe Länge b
- Eine abweichende Seite: Die andere Parallelseite hat eine unterschiedliche Länge a
- Achsensymmetrie: Symmetrisch zur Mittelsenkrechten der parallelen Seiten
- Umkreis-Existenz: Besitzt einen eindeutigen Umkreis durch alle vier Eckpunkte
- Besondere Winkelbeziehungen: Komplementäre Basiswinkel mit trigonometrischen Eigenschaften
Mathematische Besonderheiten
Die mathematischen Eigenschaften führen zu eleganten Formeln und Beziehungen:
Vereinfachte Berechnungen
Die Symmetrie ermöglicht vereinfachte Formeln, besonders für Diagonale und Umfang. Die Gleichheit von drei Seiten reduziert die Komplexität erheblich.
Trigonometrische Beziehungen
Die Winkelberechnung erfolgt über den Arccos, wobei die besonderen Seitenverhältnisse zu charakteristischen Winkeln führen.
Umkreis-Eigenschaften
Als einer der wenigen Trapez-Typen besitzt es einen Umkreis, was zu interessanten geometrischen Konstruktionen führt.
Grenzfall-Betrachtungen
Bei a = b wird es zum Rhombus, bei a = 0 zum gleichschenkligen Dreieck - wichtige Spezialfälle der Geometrie.
Konstruktive Eigenschaften
Das dreigleichseitige Trapez bietet einzigartige konstruktive Vorteile:
Stabilität und Festigkeit
- Gleichmäßige Lastverteilung durch drei gleiche Seiten
- Reduzierte Spannungskonzentrationen
- Symmetrische Kraftübertragung
- Hohe Torsionssteifigkeit
Fertigungsvorteile
- Nur zwei verschiedene Seitenlängen nötig
- Vereinfachte Werkzeugherstellung
- Reduzierte Materialvielfalt
- Modulare Bauweise möglich
Ästhetische Qualitäten
- Ausgewogene Proportionen
- Natürlich wirkende Asymmetrie
- Harmonische Formsprache
- Vielseitige Gestaltungsmöglichkeiten
Funktionale Flexibilität
- Anpassbare Proportionen durch a/b-Verhältnis
- Skalierbare Grundform
- Kombinierbarkeit mit anderen Formen
- Universelle Anwendbarkeit
Moderne Anwendungen und Trends
In der zeitgenössischen Anwendung gewinnt das dreigleichseitige Trapez an Bedeutung:
- Parametrisches Design: CAD-Systeme nutzen die klaren mathematischen Beziehungen für automatisierte Konstruktionen
- Nachhaltige Architektur: Optimierte Materialnutzung durch standardisierte Komponenten
- Digitale Fabrikation: 3D-Druck und CNC-Fertigung profitieren von den vereinfachten Geometrien
- Biomimetik: Inspiration aus natürlichen Formen mit ähnlichen Proportionen
- Smart Materials: Adaptive Strukturen nutzen die besonderen mechanischen Eigenschaften
- Modulares Bauen: Vorgefertigte Elemente für effiziente Konstruktion
Zusammenfassung
Das dreigleichseitige Trapez stellt eine einzigartige Verbindung zwischen mathematischer Eleganz und praktischer Anwendbarkeit dar. Seine besonderen Eigenschaften - drei gleiche Seiten, Achsensymmetrie und Umkreis-Existenz - machen es zu einem wertvollen Werkzeug in Geometrie, Konstruktion und Design. Die vereinfachten Berechnungsformeln und die vielseitigen Anwendungsmöglichkeiten zeigen das Potenzial dieser oft übersehenen geometrischen Form auf.
|
|