Trapez Höhe mit Winkel berechnen
Rechner und Formeln zur trigonometrischen Höhenberechnung
Trapez Höhe über Trigonometrie
Trigonometrische Höhenberechnung
Die Höhe h wird über Sinus-Funktion aus einem Schenkel und seinem Winkel berechnet. Wahlweise Seite b oder d mit entsprechenden Winkeln.
Trapez mit Winkeln
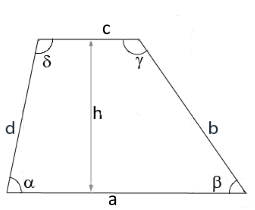
Das Diagramm zeigt ein Trapez mit den Schenkeln b und d sowie den Winkeln α, β, γ, δ.
Die Höhe h wird trigonometrisch über Sinus berechnet.
Trigonometrische Höhenberechnung
Die trigonometrische Methode nutzt die Sinus-Funktion zur direkten Höhenberechnung:
- Direkte Berechnung: Keine Zwischenschritte nötig
- Sinus-Funktion: h = Seitenlänge × sin(Winkel)
- Mehrere Optionen: Verschiedene Seiten-Winkel-Kombinationen
- Praktisch messbar: Winkel oft einfacher zu messen als Fläche
- Präzise Ergebnisse: Hohe Genauigkeit bei genauen Winkeln
- Vielseitig: Funktioniert bei allen Trapez-Formen
Sinus-Funktion im Trapez
Die Sinus-Funktion ermöglicht die direkte Höhenberechnung:
Grundprinzip
Projektion des Schenkels auf die Höhe
Rechtwinkliges Dreieck
Die Höhe bildet mit dem Schenkel und der Grundseite ein rechtwinkliges Dreieck, wodurch die Sinus-Beziehung anwendbar wird.
Praktische Anwendungen der Winkel-Methode
Die trigonometrische Höhenberechnung ist in vielen Bereichen vorteilhaft:
Vermessung & Geodäsie
- Winkelmessung mit Theodoliten
- Triangulation in der Landvermessung
- Höhenbestimmung bei unzugänglichen Objekten
- GPS-gestützte Vermessungsarbeiten
Bauwesen & Konstruktion
- Dachneigungen und Sparrenlängen
- Böschungswinkel bei Erdarbeiten
- Treppenkonstruktionen
- Brücken- und Tunnelbau
Maschinenbau & Technik
- Keilwinkel und Neigungen
- Zahnradgeometrie
- Werkzeugwinkel
- Robotik und Kinematik
Design & CAD
- Parametrische Konstruktion
- 3D-Modellierung
- Technische Zeichnungen
- Architektur-Software
Formeln zur trigonometrischen Höhenberechnung
Grundformel: Sinus-basierte Höhenberechnung
Allgemeine Form für alle Schenkel-Winkel-Kombinationen
Mit Schenkel b und Winkel β
Rechter Schenkel mit oberem Winkel
Mit Schenkel b und Winkel γ
Rechter Schenkel mit unterem Winkel
Mit Schenkel d und Winkel α
Linker Schenkel mit oberem Winkel
Mit Schenkel d und Winkel δ
Linker Schenkel mit unterem Winkel
Alternative: Höhe aus Fläche
Wenn Fläche A und parallele Seiten a, c bekannt sind. Hier verfügbar →
Trigonometrische Grundlagen
\(\sin(\text{Winkel}) = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}\)
In unserem Fall: Höhe / Schenkel
\(\text{Höhe} = \text{Schenkel} \cdot \sin(\text{Winkel})\)
Nach der Höhe aufgelöst
Grad (°) oder Radiant (rad)
Umrechnung: rad = grad × π/180
\(0° \leq \text{Winkel} \leq 180°\) für Trapeze
sin(Winkel) ist immer positiv
Rechenbeispiel
Gegeben
Gesucht: Höhe h des Trapezes
1. Sinus-Wert bestimmen
Bekannter trigonometrischer Wert
2. Höhe berechnen
Formel anwenden
3. Verifikation mit anderen Winkeln
\[h = 4 \cdot \sin(120°) = 4 \cdot \sin(180° - 60°) = 4 \cdot \sin(60°) = 3.464\]
Das Ergebnis ist identisch, da sin(120°) = sin(60°)
Die Höhe beträgt etwa 3.46 Längeneinheiten
4. Plausibilitätsprüfung
Logische Kontrolle:
• Die Höhe (3.46) ist kleiner als der Schenkel (4.0) ✓
• Bei 60° erwartet man eine Höhe von etwa 87% des Schenkels ✓
• sin(60°) ≈ 0.866, also 4 × 0.866 = 3.464 ✓
Praktische Bedeutung: Bei einem Dachsparren von 4m Länge und 60° Neigung
ergibt sich eine Gebäudehöhe von etwa 3.46m.
Trigonometrische Höhenberechnung in Theorie und Praxis
Die trigonometrische Berechnung der Trapez-Höhe verbindet klassische Geometrie mit praktischer Anwendbarkeit. Während andere Methoden umständliche Zwischenrechnungen erfordern, ermöglicht die Sinus-Funktion eine direkte und elegante Lösung. Diese Methode ist besonders wertvoll in Bereichen, wo Winkel präzise messbar sind oder als Designparameter vorgegeben werden.
Trigonometrische Grundlagen
Die Anwendung der Sinus-Funktion im Trapez basiert auf fundamentalen Prinzipien:
- Rechtwinkliges Dreieck: Die Höhe bildet mit jedem Schenkel ein rechtwinkliges Dreieck
- Sinus-Definition: sin(α) = Gegenkathete/Hypotenuse = h/Schenkel
- Auflösung nach h: h = Schenkel × sin(Winkel)
- Universalität: Funktioniert mit allen vier Winkeln des Trapezes
- Genauigkeit: Direkte Berechnung ohne Rundungsfehler durch Zwischenschritte
Winkel-Optionen und deren Bedeutung
Die vier verschiedenen Berechnungsoptionen bieten Flexibilität je nach verfügbaren Daten:
Schenkel b (rechts)
Mit den Winkeln β (oben rechts) oder γ (unten rechts). Häufig in der Praxis einfacher zugänglich, da meist von der rechten Seite gemessen wird.
Schenkel d (links)
Mit den Winkeln α (oben links) oder δ (unten links). Alternative, wenn die linke Seite des Trapezes besser zugänglich ist.
Komplementäre Winkel
Oft sind gegenüberliegende Winkel komplementär (α + γ = 180°, β + δ = 180°), was zur Verifikation genutzt werden kann.
Mess-Strategien
In der Praxis wird der am einfachsten messbare Winkel gewählt, abhängig von Zugänglichkeit und Messinstrumenten.
Praktische Mess- und Anwendungsverfahren
Die trigonometrische Höhenberechnung findet in zahlreichen praktischen Bereichen Anwendung:
Vermessungstechnik
- Theodolit-Messungen für präzise Winkelbestimmung
- Triangulation in der Geodäsie
- Laser-Entfernungsmesser mit Winkelfunktion
- GPS-gestützte Vermessung mit Neigungssensoren
Bauwesen
- Dachneigungen und Sparrenlängen berechnen
- Böschungswinkel bei Erdarbeiten
- Treppensteigungen und Podesthöhen
- Rampen für barrierefreies Bauen
Maschinenbau
- Keilwinkel und Neigungen in Getrieben
- Werkzeuggeometrie bei Schneidwerkzeugen
- Führungsschienen und Gleitbahnen
- Roboterkinematik und Gelenkwinkel
Design und Architektur
- Parametrisches Design in CAD-Systemen
- Fassadenneigungen und Sonnenschutz
- Landschaftsarchitektur und Geländemodellierung
- Bühnentechnik und Veranstaltungstechnik
Moderne Technologien und digitale Integration
Die trigonometrische Höhenberechnung profitiert von modernen Technologien:
- Smartphone-Apps: Neigungsmesser und Winkelmess-Apps für schnelle Feldmessungen
- Drohnen-Vermessung: Automatische Winkelerfassung aus Luftbildern
- 3D-Scanner: Präzise Erfassung komplexer Geometrien
- CAD-Integration: Parametrische Modelle mit automatischer Trigonometrie
- IoT-Sensoren: Kontinuierliche Überwachung von Neigungen und Winkeln
- Machine Learning: Automatische Mustererkennung in Bildauswertung
- Augmented Reality: Echtzeit-Winkelmessung und -visualisierung
Genauigkeitsbetrachtungen und Fehlerquellen
Bei der praktischen Anwendung sind verschiedene Faktoren zu beachten:
Messgenauigkeit
Die Genauigkeit der Höhe hängt direkt von der Präzision der Winkelmessung ab. Ein Fehler von 1° kann bereits erhebliche Auswirkungen haben.
Trigonometrische Stabilität
Bei sehr kleinen oder sehr großen Winkeln wird die Sinus-Funktion instabil. Optimale Ergebnisse bei Winkeln zwischen 20° und 160°.
Umgebungseinflüsse
Temperatur, Luftfeuchtigkeit und atmosphärische Bedingungen können bei präzisen Messungen berücksichtigt werden müssen.
Kalibrierung
Regelmäßige Kalibrierung der Messinstrumente ist für zuverlässige Ergebnisse unerlässlich.
Zusammenfassung
Die trigonometrische Höhenberechnung beim Trapez exemplifiziert die Eleganz mathematischer Methoden in praktischen Anwendungen. Die Direktheit der Sinus-Funktion h = Seitenlänge × sin(Winkel) macht komplexe geometrische Probleme zu lösbaren Berechnungen. Von der klassischen Vermessung bis hin zu modernen CAD-Systemen und IoT-Anwendungen zeigt diese Methode die zeitlose Relevanz trigonometrischer Grundlagen in einer digitalisierten Welt.
|
|