Trapez Diagonale f berechnen
Rechner und Formeln zur Trapez Diagonalen f über Seitenlängen und Höhe
Trapez Diagonale f Rechner
Zweite Trapez-Diagonale
Ein Trapez hat zwei Diagonalen. Die Diagonale f verbindet die anderen beiden nicht benachbarten Eckpunkte und kann aus den Seiten a, d und der Höhe h berechnet werden.
Trapez mit Diagonale f
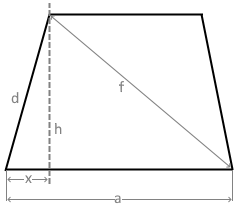
Das Diagramm zeigt ein Trapez mit den Seiten a und d, der Höhe h und der Diagonale f.
Die Diagonale f ist die zweite Diagonale des Trapezes.
|
|
Die zweite Diagonale f im Trapez
Jedes Trapez besitzt zwei Diagonalen mit unterschiedlichen Eigenschaften:
- Diagonale e: Verbindet einen Eckpunkt der oberen mit der unteren Basis
- Diagonale f: Verbindet den anderen Eckpunkt mit der gegenüberliegenden Ecke
- Unterschiedliche Längen: Bei allgemeinen Trapezen meist verschieden lang
- Gleiche Längen: Nur bei gleichschenkligen Trapezen identisch
- Schnittpunkt: Beide Diagonalen schneiden sich im Inneren
- Anwendung: Strukturelle Analyse, Verstrebungen, Design
Berechnung der Diagonale f
Die Diagonale f wird über eine andere Seitenkombination berechnet:
Unterschied zu e
- Nutzt Seiten a und d (statt a und b)
- Andere Orientierung im Trapez
- Verschiedene Projektionslänge x
- Meist andere Länge als Diagonale e
Berechnungsprinzip
- Pythagoras in rechtwinkligem Teildreieck
- Projektion x der Seite d
- Kombination mit Höhe h
- Ähnlicher Ansatz wie bei Diagonale e
Praktische Bedeutung beider Diagonalen
Beide Trapez-Diagonalen sind in verschiedenen Anwendungen wichtig:
Konstruktion & Statik
- Fachwerke: Beide Diagonalen als Verstrebungen
- Dachkonstruktionen: Verschiedene Sparren
- Brückenbau: Kreuzförmige Aussteifung
- Stahlbau: Redundante Tragstruktur
Design & Geometrie
- Architektur: Asymmetrische Gestaltung
- Möbeldesign: Trapezoidale Formen
- Landschaftsarchitektur: Wegeführung
- Industriedesign: Funktionale Geometrie
Berechnungsmethoden für Diagonale f
Die Diagonale f kann auf ähnliche Weise wie Diagonale e berechnet werden:
Pythagoras
Rechtwinkliges Teildreieck nutzen
Koordinaten
Kartesisches Koordinatensystem
Trigonometrie
Winkel und trigonometrische Funktionen
Formeln zur Berechnung der Diagonale f
Hauptformel mit Seiten a, d und Höhe h
Dabei ist: \(x = \sqrt{d^2 - h^2}\)
Berechnung von x
Horizontaler Abstand der schrägen Seite d
Alternative mit Seiten c, b
Mit \(y = \sqrt{b^2 - h^2}\)
Koordinaten-Methode
Euklidische Distanz zwischen Eckpunkten
Mit Winkel α
Cosinussatz für Winkel zwischen a und d
Schritt-für-Schritt Berechnung
\(x = \sqrt{d^2 - h^2}\)
Horizontalprojektion der Seite d
\(f = \sqrt{(a-x)^2 + h^2}\)
Pythagoras im rechtwinkligen Dreieck
Unterschied zwischen Diagonalen e und f
- Diagonale e: Nutzt Seiten a und b
- Diagonale f: Nutzt Seiten a und d
- Projektion: y für e, x für f
- Orientierung: Verschiedene Richtungen
- Längen: Meist unterschiedlich
- Anwendung: Je nach Konstruktion relevant
- Berechnung: Analoges Vorgehen
- Symmetrie: Nur bei gleichschenkligen Trapezen gleich
Rechenbeispiel
Gegeben
Gesucht: Diagonale f
1. Berechnung von x
Horizontale Projektion der schrägen Seite d
2. Berechnung der Diagonale f
Pythagoras im rechtwinkligen Teildreieck
3. Ergebnis
Die Diagonale f hat eine Länge von etwa 5.66 Einheiten
4. Vergleich mit Diagonale e
Berechnung der Diagonale e mit gleichen Werten:
Angenommen, Seite b = 5 (gleich wie d), dann:
\(y = \sqrt{5^2 - 4^2} = 3\) (gleich wie x)
\(e = \sqrt{(7-3)^2 + 4^2} = \sqrt{32} \approx 5.66\)
In diesem Beispiel sind beide Diagonalen gleich lang, da b = d.
Bei unterschiedlichen Seitenlängen b ≠ d würden sich verschiedene Diagonalenlängen ergeben.
Die Diagonale f - Geometrie und praktische Bedeutung
Die Diagonale f ist die zweite Diagonale eines Trapezes und ergänzt die Diagonale e zu einem vollständigen geometrischen Verständnis. Beide Diagonalen zusammen charakterisieren die innere Struktur des Trapezes und sind für konstruktive und analytische Anwendungen von großer Bedeutung.
Geometrische Eigenschaften der Diagonale f
Die Diagonale f unterscheidet sich von der Diagonale e durch ihre Orientierung und Berechnung:
- Alternative Verbindung: Verbindet die anderen beiden nicht benachbarten Eckpunkte
- Unterschiedliche Seitenbasis: Nutzt die Seiten a und d statt a und b
- Verschiedene Projektionen: Die Horizontalprojektion x unterscheidet sich meist von y
- Asymmetrie: Bei allgemeinen Trapezen meist andere Länge als Diagonale e
- Symmetrie-Spezialfall: Nur bei gleichschenkligen Trapezen gleich lang wie e
Berechnungsverfahren im Detail
Die Berechnung der Diagonale f folgt dem gleichen Grundprinzip wie bei e:
Pythagoras-Ansatz
Durch Projektion der Seite d auf die Grundlinie entsteht ein rechtwinkliges Dreieck, in dem die Diagonale f die Hypotenuse bildet.
Projektionsberechnung
Die Horizontalprojektion x = √(d² - h²) der schrägen Seite d ist der Schlüssel zur Lösung.
Koordinaten-Alternative
In einem Koordinatensystem kann die Diagonale f direkt über die Distanzformel berechnet werden.
Trigonometrische Methode
Bei bekanntem Winkel zwischen a und d kann der Cosinussatz angewendet werden.
Praktische Anwendungen beider Diagonalen
In der Praxis sind oft beide Diagonalen relevant und ergänzen sich:
Struktureller Ingenieurbau
- Fachwerke: Kreuzweise Verstrebung für Stabilität
- Brückenbau: Redundante Tragstrukturen
- Stahlbau: Aussteifung in beide Richtungen
- Hochbau: Rahmenversteifung
Maschinenbau
- Getriebetechnik: Verschiedene Kraftrichtungen
- Fahrzeugbau: Chassisversteifung
- Werkzeugmaschinen: Mehrrichtungs-Führungen
- Robotik: Gelenkkinematik
Architektur und Design
- Moderne Architektur: Asymmetrische Gestaltung
- Dachkonstruktionen: Verschiedene Sparrenrichtungen
- Innenarchitektur: Raumaufteilung
- Landschaftsarchitektur: Wegeführung
Wissenschaft und Technik
- Physik: Kraftzerlegung in verschiedene Richtungen
- Optik: Strahlführung und Prismen
- Elektrotechnik: Leiterplattengeometrie
- Computergrafik: Polygon-Rendering
Vergleich der Diagonalen e und f
Die beiden Diagonalen ergänzen sich und bieten unterschiedliche Perspektiven:
Gemeinsame Eigenschaften
Beide nutzen den gleichen mathematischen Ansatz (Pythagoras), teilen das Trapez in Dreiecke und schneiden sich im Inneren.
Bei gleichschenkligen Trapezen
Beide Diagonalen haben gleiche Länge und das Trapez zeigt Achsensymmetrie bezüglich der Mittelsenkrechten.
Unterschiede
Verschiedene Seitenpaare, unterschiedliche Projektionen, meist verschiedene Längen bei allgemeinen Trapezen.
Konstruktive Bedeutung
Je nach Belastungsrichtung oder Gestaltungsabsicht kann eine der Diagonalen wichtiger sein.
Historische Entwicklung
Die systematische Untersuchung von Trapez-Diagonalen entwickelte sich parallel zur Geometrie:
- Antike Geometrie: Erste Erkenntnisse über Vierecke und ihre Eigenschaften
- Mittelalterliche Mathematik: Systematisierung der Viereck-Geometrie
- Renaissance: Anwendung in Architektur und Perspektive
- Industrielle Revolution: Praktische Anwendung im Ingenieurbau
- Moderne Zeit: Computergestützte Berechnung und Visualisierung
- Gegenwart: Integration in CAD-Systeme und automatisierte Konstruktion
Zusammenfassung
Die Diagonale f ergänzt die Diagonale e zu einem vollständigen Verständnis der Trapez-Geometrie. Beide zusammen ermöglichen es, die innere Struktur eines Trapezes vollständig zu beschreiben und für praktische Anwendungen zu nutzen. Die mathematischen Berechnungsmethoden verbinden klassische Geometrie mit modernen Anwendungen und zeigen die zeitlose Relevanz geometrischer Grundlagen in einer technologisch fortgeschrittenen Welt.
|
|
|
|