Calculate Trapezoid Diagonal f
Calculator and formulas for trapezoid diagonal f using side lengths and height
Trapezoid Diagonal f Calculator
Second Trapezoid Diagonal
A trapezoid has two diagonals. The diagonal f connects the other non-adjacent vertices and can be calculated from sides a, d and the height h.
Trapezoid with Diagonal f
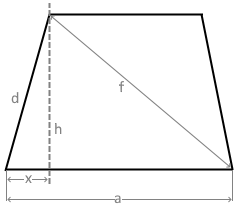
The diagram shows a trapezoid with sides a and d, height h and diagonal f.
Diagonal f is the second diagonal of the trapezoid.
The second diagonal f in a trapezoid
Every trapezoid has two diagonals with different properties:
- Diagonal e: Connects one vertex of the top base with the bottom base
- Diagonal f: Connects the other vertex with the opposite corner
- Different lengths: Usually different in general trapezoids
- Equal lengths: Only identical in isosceles trapezoids
- Intersection: Both diagonals intersect inside the trapezoid
- Applications: Structural analysis, bracing, design
Calculation of Diagonal f
The diagonal f is calculated using a different combination of sides:
Difference to e
- Uses sides a and d (instead of a and b)
- Different orientation in the trapezoid
- Different projection length x
- Usually different length than diagonal e
Calculation principle
- Pythagorean theorem in right-angled sub-triangle
- Projection x of side d
- Combination with height h
- Similar approach as for diagonal e
Practical significance of both diagonals
Both trapezoid diagonals are important in various applications:
Construction & Statics
- Trusses: Both diagonals as bracing elements
- Roof structures: different rafters
- Bridge construction: cross stiffening
- Steel structures: redundant load paths
Design & Geometry
- Architecture: asymmetric layouts
- Furniture design: trapezoidal shapes
- Landscape architecture: pathway design
- Industrial design: functional geometry
Calculation methods for Diagonal f
Diagonal f can be calculated in a similar way as diagonal e:
Pythagorean
Use right-angled sub-triangle
Coordinates
Cartesian coordinate system
Trigonometry
Angles and trigonometric functions
Formulas for calculating Diagonal f
Main formula with sides a, d and height h
Where: \(x = \sqrt{d^2 - h^2}\)
Calculation of x
Horizontal distance of the oblique side d
Alternative with sides c, b
With \(y = \sqrt{b^2 - h^2}\)
Coordinate method
Euclidean distance between vertices
With angle α
Law of cosines for angle between a and d
Step-by-step calculation
\(x = \sqrt{d^2 - h^2}\)
Horizontal projection of side d
\(f = \sqrt{(a-x)^2 + h^2}\)
Pythagorean theorem in right triangle
Difference between diagonals e and f
- Diagonal e: Uses sides a and b
- Diagonal f: Uses sides a and d
- Projection: y for e, x for f
- Orientation: Different directions
- Lengths: Usually different
- Application: Relevant depending on construction
- Calculation: Analogous approach
- Symmetry: Equal only in isosceles trapezoids
Calculation Example
Given
Find: Diagonal f
1. Calculation of x
Horizontal projection of oblique side d
2. Calculation of diagonal f
Pythagorean theorem in right sub-triangle
3. Result
Diagonal f has a length of approximately 5.66 units
4. Comparison with diagonal e
Calculation of diagonal e with same values:
Assume side b = 5 (same as d), then:
\(y = \sqrt{5^2 - 4^2} = 3\) (same as x)
\(e = \sqrt{(7-3)^2 + 4^2} = \sqrt{32} \approx 5.66\)
In this example both diagonals are equal because b = d.
With different side lengths b ≠ d the diagonals would differ.
Diagonal f - Geometry and practical relevance
The diagonal f is the second diagonal of a trapezoid and complements diagonal e to provide a complete geometric understanding. Both diagonals together characterize the trapezoid's internal structure and are important for constructive and analytical applications.
Geometric properties of diagonal f
Diagonal f differs from diagonal e by orientation and calculation:
- Alternative connection: Connects the other two non-adjacent vertices
- Different side basis: Uses sides a and d instead of a and b
- Different projections: The horizontal projection x usually differs from y
- Asymmetry: Typically different length than diagonal e in general trapezoids
- Symmetry special case: Equal to e only in isosceles trapezoids
Calculation methods in detail
The calculation of diagonal f follows the same basic principle as for e:
Pythagorean approach
By projecting side d onto the base line a right triangle is formed, where diagonal f is the hypotenuse.
Projection calculation
The horizontal projection x = √(d² - h²) of the oblique side d is the key to the solution.
Coordinate alternative
In a coordinate system the diagonal f can be calculated directly using the distance formula.
Trigonometric method
With a known angle between a and d the law of cosines can be used.
Practical applications of both diagonals
In practice both diagonals are often relevant and complement each other:
Structural engineering
- Trusses: Cross bracing for stability
- Bridge construction: Redundant load paths
- Steel structures: Stiffening in both directions
- High-rise buildings: Frame stiffening
Mechanical engineering
- Gear technology: Different force directions
- Vehicle construction: Chassis stiffening
- Machine tools: Multi-direction guides
- Robotics: Joint kinematics
Architecture and design
- Modern architecture: Asymmetric design
- Roof structures: Different rafter directions
- Interior design: Space division
- Landscape architecture: Pathway planning
Science and technology
- Physics: Force decomposition in different directions
- Optics: Ray guidance and prisms
- Electrical engineering: PCB geometry
- Computer graphics: Polygon rendering
Comparison of diagonals e and f
The two diagonals complement each other and offer different perspectives:
Common properties
Both use the same mathematical approach (Pythagorean), divide the trapezoid into triangles and intersect inside it.
In isosceles trapezoids
Both diagonals have equal length and the trapezoid shows axial symmetry about the mid-perpendicular.
Differences
Different side pairs, different projections, usually different lengths in general trapezoids.
Constructive significance
Depending on load direction or design intent, one diagonal may be more important.
Historical development
The systematic study of trapezoid diagonals developed alongside geometry:
- Ancient geometry: Early findings about quadrilaterals and their properties
- Medieval mathematics: Systematization of quadrilateral geometry
- Renaissance: Application in architecture and perspective
- Industrial revolution: Practical use in engineering
- Modern era: Computer-aided computation and visualization
- Present: Integration in CAD systems and automated design
Summary
Diagonal f complements diagonal e to provide a complete understanding of trapezoid geometry. Together they allow a full description of the trapezoid's internal structure and are usable for practical applications. The mathematical methods link classical geometry with modern applications and demonstrate the timeless relevance of geometric fundamentals in a technologically advanced world.
|
|