Calculate Trapezoid Diagonal e with Angle
Calculator and formulas for trapezoid diagonal e using side lengths and angle
Trapezoid Diagonal e (Angle Method)
Angle-based Calculation
With known side lengths a and b and an angle β, the diagonal e can be calculated directly using the law of cosines, without needing the height.
Trapezoid with Angle β
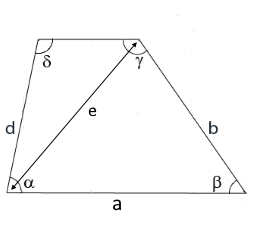
The diagram shows a trapezoid with sides a and b and angle β.
Diagonal e is calculated using the law of cosines.
Angle-based Diagonal Calculation
The angle-based method for calculating trapezoid diagonals offers advantages:
- Direct approach: No height calculation required
- Law of cosines: Proven trigonometric method
- Flexibility: Works with various trapezoid shapes
- Accuracy: Precise results with known angles
- Application: Particularly useful in surveying
- Supplement: Alternative to height-based calculation
Angle β in the Trapezoid
The angle β plays a central role in the calculation:
Definition
- Angle between sides a and b
- Measured in degrees (°) or radians
- Typically between 0° and 180°
- Determines the shape of the trapezoid
Influence on Diagonal
- Cosine of the angle determines the length
- At 90° it corresponds to Pythagorean theorem
- Acute angles result in longer diagonals
- Obtuse angles shorten the diagonal
Law of Cosines in Trapezoids
The law of cosines enables direct calculation of the diagonal:
Formula
Generalization of the Pythagorean theorem
Application
- Valid for all triangles and trapezoid parts
- Reduces to Pythagorean theorem when β=90°
- Considers angle geometry
- Direct path without intermediate steps
Comparison of Calculation Methods
There are different approaches to calculating trapezoid diagonals:
With Angle
Apply law of cosines directly
With Height
Pythagorean theorem in sub-triangle
Coordinates
Analytical geometry
Formulas for Angle-based Diagonal Calculation
Main Formula: Law of Cosines
Diagonal from two sides and the included angle
Angle in Radians
Conversion from degrees to radians
Special Case β = 90°
Reduces to Pythagorean theorem
Alternative Form
Without square root for intermediate calculations
Angle between Other Sides
With known sides c, d and angle δ
Step-by-Step Calculation
If necessary, convert degrees to radians
Many calculators accept both units
\(\cos(\beta)\) of the given angle
Apply trigonometric function
\(e^2 = a^2 + b^2 - 2ab\cos(\beta)\)
Insert values into law of cosines
\(e = \sqrt{e^2}\)
Square root for final result
Important Angle Values
- cos(0°) = 1: Maximum cosine value
- cos(60°) = 0.5: Commonly used value
- cos(90°) = 0: Right angle
- cos(120°) = -0.5: Obtuse angle
- cos(180°) = -1: Minimum cosine value
- cos(30°) ≈ 0.866: Common reference value
- cos(45°) ≈ 0.707: Half of right angle
- cos(135°) ≈ -0.707: Standard obtuse angle
Calculation Example
Given
Find: Diagonal e
1. Calculate cosine
Known trigonometric value
2. Substitute values
Apply law of cosines
3. Final result
Diagonal e has a length of approximately 5.29 units
4. Verification and Plausibility
Plausibility check:
• The diagonal (5.29) lies between the side lengths 4 and 6 ✓
• At 60° the cosine is positive (0.5), causing moderate shortening ✓
• Without angle term would be √(36+16) = √52 ≈ 7.21, with angle smaller ✓
Alternative calculation: At β=90° would be e = √(36+16) = √52 ≈ 7.21
Since 60° < 90°, cos(60°) > 0, thus e < 7.21 ✓
Angle-based Trapezoid Diagonals in Theory and Practice
The angle-based calculation of trapezoid diagonals significantly expands geometric possibilities. While the height-based method uses right-angled subdivision, the law of cosines enables direct calculation from side lengths and angles - an approach that is particularly valuable in surveying and mechanical engineering.
Law of Cosines - Fundamental Extension
The law of cosines is one of the most important generalizations of the Pythagorean theorem:
- General validity: Works for all triangles, not just right-angled ones
- Angle integration: Explicitly considers angle geometry
- Pythagorean theorem as special case: At 90° the formula reduces to the classical Pythagorean theorem
- Versatility: Enables calculations with different parameter types
- Practical relevance: Directly applicable without intermediate steps
Angle Geometry in Trapezoids
Angles play a fundamental role in trapezoid geometry:
Interior Angle Properties
The sum of all interior angles is 360°. Opposite angles at parallel sides are supplementary (add up to 180°).
Symmetry Relationships
In isosceles trapezoids, the base angles are pairwise equal, which simplifies calculation.
Practical Measurability
Angles are often easier to measure than heights, especially in surveying and with inaccessible objects.
Constructive Significance
In construction, angles are often given as primary parameters from which other quantities are derived.
Practical Applications of the Angle Method
Angle-based diagonal calculation finds application in many areas:
Surveying and Cartography
- Triangulation: Distance determination via angles
- Topographic surveys: Terrain surveying
- GPS-based measurements: Satellite geometry
- Cadastral surveying: Property boundaries
Civil Engineering
- Roof construction: Rafter calculation
- Bridge building: Truss elements
- Steel construction: Connection diagonals
- Concrete construction: Formwork geometry
Mechanical Engineering
- Gear technology: Lever geometry
- Robotics: Joint kinematics
- Vehicle technology: Suspension geometry
- Machine tools: Guide calculation
Navigation and Orientation
- Aviation: Flight route calculation
- Navigation: Course determination
- Military: Target acquisition and bearing
- Astronomy: Star position determination
Trigonometrical Fundamentals
Application of the law of cosines requires solid understanding of trigonometry:
Cosine Function
The cosine describes the ratio of adjacent side to hypotenuse. For obtuse angles (> 90°) it becomes negative, which is mathematically correctly considered.
Angle Units
Degrees (360° = full circle) and radians (2π = full circle) are the common units. Most calculators can switch between both.
Accuracy and Precision
The accuracy of angle specification determines the precision of the result. Small angle errors can have large effects on the calculated diagonal.
Periodicity
Trigonometric functions are periodic. For trapezoid calculations, angles between 0° and 180° are normally relevant.
Comparison of Calculation Methods
Different methods have different advantages and disadvantages:
Angle Method (Law of Cosines)
Advantages:
- Direct calculation without intermediate steps
- Angles often easier to measure than heights
- Works with all trapezoid shapes
- Mathematically elegant and precise
Disadvantages:
- Requires trigonometric knowledge
- Angle measurement can be error-prone
- Calculator-dependent for complex calculations
Height Method (Pythagorean)
Advantages:
- Intuitive and geometrically understandable
- Uses familiar Pythagorean relationships
- Heights often directly measurable
- Less trigonometric knowledge needed
Disadvantages:
- Multiple calculation steps required
- Height measurement not always possible
- Projection calculation as intermediate step
Historical Development
The development of angle-based calculations has a long history:
- Ancient trigonometry: First systematic angle calculations by Greek and Islamic mathematicians
- Law of cosines: Generalization of Pythagorean theorem, fully developed in medieval times
- Surveying: Practical application in navigation and cartography since the Renaissance
- Industrial Revolution: Mechanical engineering and construction as new application fields
- Modern era: Computer-aided calculations and GPS technology
- Digital age: Automated calculations in CAD and simulation
Extended Applications
Modern applications go far beyond simple trapezoid calculations:
- 3D modeling: Spatial trapezoid structures in CAD systems
- Finite element analysis: Trapezoidal elements in structural calculation
- Computer graphics: Polygon rendering and geometric transformations
- Robotics: Inverse kinematics for articulated robots
- Architecture: Parametric design and geometric optimization
- Physical simulation: Collision detection and motion calculation
Summary
The angle-based calculation of trapezoid diagonals using the law of cosines represents an elegant and practical alternative to the height-based method. It combines mathematical elegance with practical applicability and is particularly valuable when angles are easier to determine than heights. The method forms a bridge between basic geometry and advanced trigonometry and demonstrates the versatility of mathematical approaches in problem solving.
Alternative Calculation Methods
Besides the angle-based method, other approaches exist for calculating trapezoid diagonals:
Height-based Calculation
When the height h is known, the diagonal can be calculated via right-angled sub-triangles:
Step 1: Calculate projection
Horizontal projection of the oblique side
Step 2: Determine diagonal
Pythagorean theorem in right sub-triangle
Coordinate-based Calculation
Placing the trapezoid in a coordinate system enables analytical calculation:
Apply distance formula
Euclidean distance between the diagonal's vertices
Method Comparison
Angle Method
Input: Sides a, b + Angle β
Formula: Law of cosines
Advantage: Direct, no height needed
Disadvantage: Trigonometry required
Height Method
Input: Sides a, b + Height h
Formula: Pythagorean theorem
Advantage: Intuitive, familiar
Disadvantage: Multiple steps
Coordinate Method
Input: Vertex coordinates
Formula: Distance formula
Advantage: Universally applicable
Disadvantage: Coordinate setup needed
|
|