Calculate Isosceles Trapezoid
Calculator and formulas for the isosceles (symmetrical) trapezoid
Isosceles Trapezoid Calculator
Isosceles trapezoid
An isosceles (symmetrical) trapezoid has equal legs (b = d) and is symmetric about the mid-perpendicular. Calculation possible using sides and height or sides and angle.
Isosceles Trapezoid
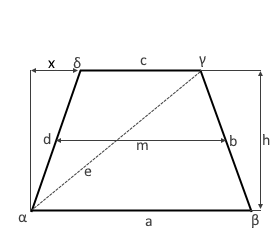
The diagram shows an isosceles trapezoid with equal legs (b = d).
The axis of symmetry is perpendicular through the middle of the parallel sides.
Properties of the isosceles trapezoid
An isosceles (symmetrical) trapezoid has special geometric properties:
- Equal legs: b = d (slanted sides have equal length)
- Axis of symmetry: Perpendicular through the midpoint of the parallel sides
- Equal base angles: α = β and γ = δ
- Equal diagonals: Both diagonals have the same length
- Axis symmetry: Reflection along the mid-perpendicular
- Special formulas: Simplified calculations are possible
Formulas for the isosceles trapezoid
Side lengths
Basic side calculations
Area and perimeter
Since b = d the perimeter simplifies
Angles
Symmetry: α = β and γ = δ
Diagonals and height
Both diagonals have equal length
Calculation example
Given
Find: All parameters of the isosceles trapezoid
1. Middle width and area
Basic calculations
2. Legs via excess
Calculation of the equal legs
3. Compute angles
Symmetric angle pairing
4. Perimeter and diagonals
All symmetry properties satisfied
Applications of the isosceles trapezoid
Isosceles trapezoids are frequently used due to their special properties:
Architecture & Design
- Roof constructions with even inclination
- Symmetric window and door openings
- Bridge arches and vaults
- Stair railings and balustrades
Engineering & Production
- Gear wheels with symmetric profiles
- V-belt pulleys and belt drives
- Flow channels with optimal distribution
- Tool cutting edges and milling profiles
The isosceles trapezoid in geometry
To compute the isosceles trapezoid (also called symmetric trapezoid) provide either sides a and c together with the height, or sides a and d together with the angle Alpha. The isosceles trapezoid is a special case of the general trapezoid with distinct symmetry properties.
The equality of the legs (b = d) leads to simplified calculation formulas and special geometric properties such as equal diagonals and symmetric angles. These properties make the isosceles trapezoid an important geometric form in architecture, engineering and design.
For further trapezoid computations there are specialized calculators available optimized for specific use cases.
|
|