Trapez Höhe aus Fläche berechnen
Rechner und Formeln zur Höhenberechnung aus Fläche und parallelen Seiten
Trapez Höhe aus Fläche Rechner
Inverse Flächenberechnung
Die Höhe h wird aus der bekannten Fläche A und den parallelen Seiten a und c berechnet. Dies ist die Umkehrung der Standard-Flächenformel.
Trapez mit Höhe h
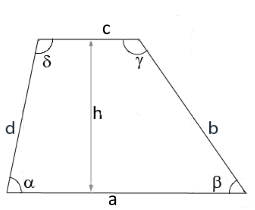
Das Diagramm zeigt ein Trapez mit den parallelen Seiten a und c sowie der gesuchten Höhe h.
Die Höhe wird aus der bekannten Fläche rückgerechnet.
Höhenberechnung aus der Fläche
Die inverse Berechnung der Trapez-Höhe ist eine wichtige Anwendung:
- Bekannte Größen: Fläche A und parallele Seiten a, c
- Gesuchte Größe: Höhe h des Trapezes
- Umkehrproblem: Rückrechnung aus der Flächenformel
- Praktische Anwendung: Konstruktion und Design
- Kontrollrechnung: Verifikation von Berechnungen
- Ingenieurwesen: Dimensionierung von Bauteilen
Umkehrung der Flächenformel
Die Herleitung der Höhenformel aus der bekannten Flächenformel:
Ausgangspunkt
Standard Trapez-Flächenformel
Umformung nach h
Nach h aufgelöste Formel
Alternative: Höhe über Winkel
Alternative Berechnungsmethoden für die Trapez-Höhe:
Mit Seite b und Winkel
Über Schenkel b und seine Winkel
Mit Seite d und Winkel
Über Schenkel d und seine Winkel
Praktische Anwendungen der Höhenberechnung
Die Höhenberechnung aus der Fläche ist in vielen Bereichen wichtig:
Konstruktion & Bauwesen
- Dimensionierung von Dachkonstruktionen
- Berechnung von Böschungshöhen
- Fundament- und Kellerplanung
- Raumhöhen bei trapezoidalen Grundrissen
Technik & Produktion
- Blechdicke bei gegebener Querschnittsfläche
- Kanalhöhen in der Strömungstechnik
- Profilhöhen im Maschinenbau
- Werkzeuggeometrie und Spannung
Landwirtschaft & Umwelt
- Damm- und Deichhöhen
- Bewässerungskanäle
- Terrassierungen im Hangbau
- Kompostmieten und Lagerstätten
Qualitätskontrolle
- Rückrechnung zur Verifikation
- Toleranzprüfung bei Bauteilen
- Dimensionskontrolle
- Fertigungsüberwachung
Formeln zur Höhenberechnung beim Trapez
Hauptformel: Höhe aus Fläche
Höhe aus bekannter Fläche A und parallelen Seiten a, c
Herleitung Schritt 1
Standard Trapez-Flächenformel
Herleitung Schritt 2
Beide Seiten mit 2 multipliziert
Alternative: Höhe über Winkel (Seite b)
Mit Schenkel b und seinen Winkeln β oder γ
Alternative: Höhe über Winkel (Seite d)
Mit Schenkel d und seinen Winkeln α oder δ
Herleitung der Hauptformel
\(A = \frac{(a + c) \cdot h}{2}\)
Standard Trapez-Flächenformel
\(2A = (a + c) \cdot h\)
Nenner eliminieren
\(h = \frac{2A}{a + c}\)
Nach h auflösen
\(h = \frac{2 \cdot A}{a + c}\)
Höhe aus Fläche und Parallelseiten
Anwendungshinweise
- Flächenformel: Wenn Fläche und Parallelseiten bekannt sind
- Winkelformel: Wenn Schenkel und Winkel bekannt sind
- Verifikation: Beide Methoden zur Kontrolle verwenden
- Einheiten beachten: Konsistente Maßeinheiten verwenden
- Plausibilität: Ergebnis auf Sinnhaftigkeit prüfen
- Rundung: Angemessene Dezimalstellen wählen
Rechenbeispiel
Gegeben
Gesucht: Höhe h des Trapezes
1. Formel anwenden
Werte in die Höhenformel einsetzen
2. Berechnung
Rechenschritte ausführen
3. Verifikation
\[A = \frac{(a + c) \cdot h}{2} = \frac{(6 + 5) \cdot 5.45}{2} = \frac{11 \cdot 5.45}{2} = \frac{59.95}{2} \approx 30\]
Die Kontrolle bestätigt das Ergebnis - die berechnete Höhe ist korrekt
4. Alternative Berechnung (falls Winkel bekannt)
Angenommen, Schenkel b = 6 und Winkel β = 65°:
\(h = b \cdot \sin(\beta) = 6 \cdot \sin(65°) = 6 \cdot 0.906 \approx 5.44\)
Das Ergebnis stimmt mit der flächenbasierten Berechnung überein.
Praktischer Hinweis: In der Praxis sind oft Fläche und Parallelseiten einfacher
messbar als Winkel, daher ist die flächenbasierte Methode häufig vorzuziehen.
Höhenberechnung aus der Fläche in Theorie und Praxis
Die Berechnung der Trapez-Höhe aus der Fläche ist ein klassisches Beispiel für inverse mathematische Problemstellungen. Während die direkte Flächenberechnung aus Höhe und Parallelseiten intuitiv verständlich ist, erfordert die Rückrechnung der Höhe aus bekannter Fläche algebraische Umformung und findet vielfältige praktische Anwendung in Konstruktion, Design und Qualitätskontrolle.
Mathematische Grundlagen der Umkehrung
Die Herleitung der Höhenformel zeigt fundamentale algebraische Prinzipien:
- Ausgangsgleichung: A = (a+c)·h/2 als bekannte Flächenformel
- Algebraische Umformung: Systematisches Auflösen nach der gesuchten Variablen h
- Inverse Operation: Von Multiplikation und Division zur umgekehrten Berechnung
- Eindeutigkeit: Bei positiven Werten für A, a und c ist die Lösung eindeutig bestimmt
- Dimensionsanalyse: [h] = [A]/[L] ergibt korrekte Längeneinheit
Praktische Bedeutung der inversen Berechnung
Die Höhenberechnung aus der Fläche löst reale Ingenieursprobleme:
Konstruktive Anwendungen
In der Praxis ist oft die benötigte Fläche vorgegeben (z.B. Querschnittsfläche für Tragfähigkeit), und die Höhe muss entsprechend dimensioniert werden.
Optimierungsprobleme
Bei Materialoptimierung oder Kosteneinsparung werden Querschnitte bei gegebener Fläche hinsichtlich der Höhe optimiert.
Qualitätskontrolle
Rückrechnung zur Verifikation: Aus gemessener Fläche wird die theoretische Höhe berechnet und mit der tatsächlichen verglichen.
Reverse Engineering
Bei der Analyse bestehender Konstruktionen werden aus bekannten Eigenschaften unbekannte Abmessungen ermittelt.
Vergleich der Berechnungsmethoden
Verschiedene Ansätze zur Höhenbestimmung haben spezifische Vor- und Nachteile:
Flächenbasierte Methode
- Vorteile: Direkte Messbarkeit der Fläche
- Genauigkeit: Hohe Präzision bei planimetrischen Verfahren
- Anwendung: Besonders bei komplexen Querschnitten
- Werkzeuge: CAD-Programme, Planimeter, Bildanalyse
Winkelbasierte Methode
- Vorteile: Direkte trigonometrische Berechnung
- Messaufwand: Benötigt Winkelmessungen
- Anwendung: Bei zugänglichen Winkeln
- Werkzeuge: Theodolit, Winkelmesser, Laser-Tools
Moderne Anwendungen und Technologien
Die Höhenberechnung aus der Fläche profitiert von modernen Technologien:
Digitale Vermessung
- 3D-Scanner für präzise Flächenerfassung
- Drohnen-basierte Photogrammetrie
- Laser-Distanzmessung
- GPS-gestützte Feldvermessung
CAD/CAM Integration
- Automatische Querschnittsberechnung
- Parametrische Modellierung
- Optimierungsalgorithmen
- Simulationsgestützte Auslegung
Qualitätssicherung
- Automatisierte Messverfahren
- Statistische Prozesskontrolle
- Inline-Messtechnik
- Machine Learning für Mustererkennung
BIM und Industrie 4.0
- Building Information Modeling
- IoT-Sensoren für Überwachung
- Predictive Maintenance
- Digitale Zwillinge
Fehlerquellen und Genauigkeitsbetrachtungen
Bei der praktischen Anwendung sind verschiedene Aspekte zu beachten:
Messgenauigkeit
Die Genauigkeit der Höhenberechnung hängt direkt von der Präzision der Flächenmessung und der Bestimmung der Parallelseiten ab.
Rundungsfehler
Bei iterativen Berechnungen können sich Rundungsfehler akkumulieren - angemessene Dezimalstellenzahl wählen.
Modellannahmen
Die Formel setzt perfekte Parallelität voraus - bei realen Bauteilen sind Toleranzen zu berücksichtigen.
Einheitenkonsistenz
Besonders bei Flächenmaßen (m²) und Längenmaßen (m) ist auf korrekte Einheitenumrechnung zu achten.
Zusammenfassung
Die Berechnung der Trapez-Höhe aus der Fläche exemplifiziert die Eleganz algebraischer Umformungen und deren praktische Relevanz. Von der theoretischen Herleitung über vielfältige Anwendungen bis hin zu modernen digitalen Implementierungen zeigt diese inverse Problemstellung die Verbindung zwischen mathematischer Theorie und ingenieurstechnischer Praxis. Die Formel h = 2A/(a+c) ist nicht nur ein Berechnungswerkzeug, sondern ein Beispiel für die Kraft mathematischen Denkens in der Lösung realer Probleme.
|
|