Rechtwinkliges Trapez berechnen
Rechner und Formeln für Trapeze mit rechtem Winkel
Rechtwinkliges Trapez Rechner
Rechtwinkliges Trapez-Form
Ein rechtwinkliges Trapez hat zwei rechte Winkel an einer Seite. Eine Seite steht senkrecht auf beiden parallelen Seiten.
Rechtwinkliges Trapez
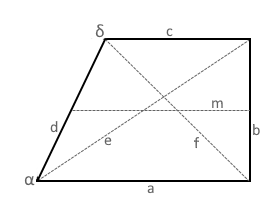
Das Diagramm zeigt ein rechtwinkliges Trapez mit zwei rechten Winkeln.
Die Seite b steht senkrecht auf den parallelen Seiten a und c.
Das rechtwinklige Trapez
Ein rechtwinkliges Trapez ist eine besondere Form des Trapezes:
- Zwei rechte Winkel: An einer Seite befinden sich zwei 90°-Winkel
- Senkrechte Seite: Eine Seite steht senkrecht auf beiden Parallelseiten
- Vereinfachte Geometrie: Einfachere Berechnungen durch rechte Winkel
- Praktische Bedeutung: Häufig in Architektur und Technik
- Pythagoras anwendbar: Für Diagonalen und schräge Seite
- Einfache Flächenberechnung: Höhe ist direkt messbar
Besondere Eigenschaften rechter Winkel
Die rechten Winkel bringen besondere geometrische Vorteile:
Geometrische Vorteile
- Höhe ist direkt eine Seitenlänge
- Keine trigonometrischen Berechnungen nötig
- Einfache Koordinaten-Darstellung möglich
- Rechtwinkliges Dreieck für Diagonalen
Praktische Messbarkeit
- Rechte Winkel einfach messbar
- Wasserwaage und Lot anwendbar
- Präzise Konstruktion möglich
- Standard-Messtechnik ausreichend
Pythagoras im rechtwinkligen Trapez
Der Satz des Pythagoras ist vielfach anwendbar:
Diagonalen berechnen
Direkte Anwendung des Pythagoras
Schräge Seite d
Über die Differenz der Parallelseiten
Praktische Anwendungen rechtwinkliger Trapeze
Rechtwinklige Trapeze finden vielfältige praktische Anwendung:
Bauwesen & Architektur
- Dachkonstruktionen und Pultdächer
- Treppenwangen und Podeste
- Fenster- und Türöffnungen
- Rampen und Auffahrten
Technik & Maschinenbau
- Blechprofile und Träger
- Führungsschienen
- Gehäusekonstruktionen
- Werkzeugmaschinen-Komponenten
Fahrzeugbau
- Karosserie-Querschnitte
- Windschutzscheiben-Rahmen
- Spoiler und Aerodynamik-Teile
- Nutzfahrzeug-Aufbauten
Wasserbau & Tiefbau
- Kanäle und Gräben
- Böschungen und Dämme
- Brückenpfeiler
- Tunnelquerschnitte
Formeln für das rechtwinklige Trapez
Seite a (aus d und b)
Pythagoras + Parallelseiten-Beziehung
Seite b (Höhe)
Pythagoras aus schräger Seite d
Seite c (aus a und d)
Umkehrung der Formel für a
Seite d (schräg)
Pythagoras im rechtwinkligen Dreieck
Diagonale e
Pythagoras mit a und Höhe b
Diagonale f
Pythagoras mit c und Höhe b
Mittlere Breite m
Arithmetisches Mittel der Parallelseiten
Flächeninhalt A
Höhe b mal mittlere Breite
Umfang P
Summe aller vier Seiten
Winkel α
Über Cosinussatz berechnet
Rechenbeispiel
Gegeben
Gesucht: Alle Eigenschaften des rechtwinkligen Trapezes
1. Schräge Seite d berechnen
Pythagoras im rechtwinkligen Dreieck
2. Diagonalen berechnen
Pythagoras für beide Diagonalen
3. Fläche und mittlere Breite
Standardformeln für Trapeze
4. Umfang
Summe aller Seitenlängen
5. Zusammenfassung aller Ergebnisse
Vollständige Charakterisierung des rechtwinkligen Trapezes
Das rechtwinklige Trapez in Theorie und Praxis
Das rechtwinklige Trapez stellt eine besonders praktische und häufig anzutreffende geometrische Form dar. Mit seinen zwei rechten Winkeln verbindet es die Einfachheit rechtwinkliger Geometrie mit der Flexibilität trapezoidaler Formen. Diese Kombination macht es zu einem bevorzugten Element in Architektur, Technik und Design.
Geometrische Eigenschaften und Vorteile
Die besonderen Eigenschaften des rechtwinkligen Trapezes ergeben sich aus der Kombination von Parallelität und Rechtwinkligkeit:
- Zwei rechte Winkel: An einer Seite des Trapezes befinden sich zwei 90°-Winkel
- Senkrechte Seite: Eine Seite steht senkrecht auf beiden parallelen Seiten und bildet die direkt messbare Höhe
- Pythagoras-Anwendbarkeit: Für Diagonalen und schräge Seite direkter Einsatz des Satzes
- Vereinfachte Berechnungen: Keine trigonometrischen Funktionen für Grundberechnungen nötig
- Eindeutige Konstruktion: Aus drei Seiten ist das Trapez vollständig bestimmt
Mathematische Eleganz
Die mathematischen Beziehungen im rechtwinkligen Trapez zeigen besondere Eleganz:
Pythagoras-Anwendungen
Der Satz des Pythagoras findet mehrfache Anwendung: für beide Diagonalen (e = √(a²+b²), f = √(c²+b²)) und für die schräge Seite d = √((a-c)²+b²).
Direkte Höhe
Die senkrechte Seite b ist gleichzeitig die Höhe des Trapezes, was die Flächenberechnung A = b(a+c)/2 vereinfacht.
Koordinaten-System
Rechtwinklige Trapeze lassen sich optimal in kartesischen Koordinatensystemen darstellen und berechnen.
Symmetrie-Eigenschaften
Bei a = c wird es zum Rechteck, die Formeln bleiben gültig und zeigen die Allgemeinheit des Ansatzes.
Praktische Anwendungen und Konstruktion
Rechtwinklige Trapeze finden breite praktische Anwendung aufgrund ihrer konstruktiven Vorteile:
Bauwesen und Architektur
- Pultdächer: Einfache Entwässerung bei rechtwinkliger Konstruktion
- Treppenwangen: Rechte Winkel für stabile Verbindungen
- Rampen: Definierte Steigung mit senkrechten Anschlüssen
- Fensterlaibungen: Rechtwinklige Einbausituation
Maschinenbau
- Profilträger: Optimierte Steifigkeit bei einfacher Fertigung
- Führungsschienen: Rechtwinklige Aufnahmen
- Gehäusekonstruktionen: Rechte Winkel für Montage
- Werkzeugmaschinen: Präzise rechtwinklige Referenzen
Fahrzeug- und Gerätebau
- Karosserie-Profile: Aerodynamik mit rechtwinkligen Anbindungen
- Nutzfahrzeuge: Ladeboden mit schräger Rückwand
- Möbeldesign: Moderne Formen mit praktischen Winkeln
- Elektronik-Gehäuse: Platinen-Aufnahme mit Schrägstellung
Wasserbau und Tiefbau
- Kanäle: Senkrechte Wände mit schräger Sohle
- Böschungen: Rechtwinklige Übergänge
- Brückenpfeiler: Vertikale Kanten mit Schrägung
- Tunnelprofile: Standard-Querschnitte
Moderne CAD-Integration und Parametrisierung
In der digitalen Konstruktion bieten rechtwinklige Trapeze besondere Vorteile:
- Parametrische Modellierung: Einfache Definition über drei Parameter (zwei Parallelseiten + Höhe oder schräge Seite)
- Constraint-basiertes Design: Rechte Winkel als natürliche Zwangsbedingungen
- Fertigungsgerechte Konstruktion: Rechte Winkel entsprechen Standard-Fertigungsverfahren
- Materialeinsparung: Optimierungspotential durch trapezoidale statt rechteckiger Querschnitte
- Simulation und FEM: Einfache Vernetzung durch rechtwinklige Struktur
- Rapid Prototyping: 3D-Druck profitiert von rechtwinkligen Geometrien
Messtechnik und Qualitätskontrolle
Die besonderen geometrischen Eigenschaften erleichtern Messung und Kontrolle:
Messverfahren
Rechte Winkel sind mit Standard-Messtechnik (Wasserwaage, Winkel, Lot) präzise messbar. Die senkrechte Seite ist direkt als Höhe messbar.
Toleranzen
Abweichungen von der Rechtwinkligkeit sind leicht erkennbar und messbar, was die Qualitätskontrolle vereinfacht.
Kalibrierung
Rechtwinklige Trapeze eignen sich als Referenzobjekte für Messgeräte und Koordinatenmessmaschinen.
Automatisierung
Bildverarbeitung und automatische Messsysteme erkennen rechte Winkel zuverlässig.
Zusammenfassung
Das rechtwinklige Trapez vereint geometrische Eleganz mit praktischer Anwendbarkeit. Die Kombination aus rechten Winkeln und trapezoidaler Form ermöglicht sowohl einfache Berechnungen als auch vielseitige konstruktive Lösungen. Von der klassischen Baugeometrie bis hin zu modernen CAD-Systemen zeigt es die zeitlose Relevanz grundlegender geometrischer Formen in einer technologisierten Welt. Die direkten Pythagoras-Anwendungen und die messbare Rechtwinkligkeit machen es zu einem bevorzugten Element in Ingenieurwesen und Design.
|
|