Trapez online berechnen
Onlinerechner und Formeln zur Berechnung eines Trapezes
Trapez Rechner
Trapez-Berechnung
Zum Berechnen des Trapezes werden entweder die Seiten a und c, sowie die Höhe und der Überstand x eingegeben; alternativ kann ein Winkel und 3 Seitenlängen angegeben werden.
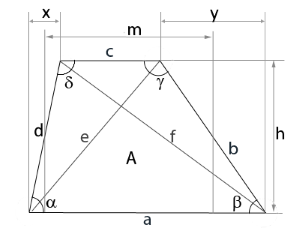
Trapez-Diagramm
Das Diagramm zeigt ein allgemeines Trapez mit allen Parametern.
Die Berechnung erfolgt über verschiedene Kombinationen von Seiten, Winkeln und Höhe.
Berechnungsmethoden für das Trapez
Der Trapez-Rechner bietet verschiedene Berechnungsmethoden je nach verfügbaren Parametern:
- Überstand-Methode: Seiten a, c, Höhe h und Überstand x
- Winkel α/δ-Methode: Drei Seiten und Winkel α oder δ
- Winkel β/γ-Methode: Drei Seiten und Winkel β oder γ
- Automatische Berechnung: Alle fehlenden Parameter werden ermittelt
- Vollständige Ergebnisse: Seiten, Winkel, Fläche, Umfang, Diagonalen
- Präzise Formeln: Trigonometrische und geometrische Berechnungen
Formeln zum Trapez
Seitenlängen
Grundlegende Seitenberechnungen
Fläche und Umfang
Flächen- und Umfangsberechnungen
Winkel
Winkelbeziehungen im Trapez
Diagonalen und Überstände
Diagonalen und horizontale Überstände
Rechenbeispiel
Gegeben (Überstand-Methode)
Gesucht: Alle Parameter des Trapezes
1. Schenkel berechnen
Berechnung der schrägen Seiten
2. Fläche und Umfang
Flächen- und Umfangsberechnung
3. Winkel berechnen
Alle vier Winkel des Trapezes
4. Diagonalen
Alle geometrischen Parameter ermittelt
Praktische Anwendungen der Trapez-Berechnung
Die allgemeine Trapez-Berechnung findet in vielen technischen und wissenschaftlichen Bereichen Anwendung:
Bauwesen & Architektur
- Dachkonstruktionen mit variablen Neigungen
- Fundamentquerschnitte und Böschungen
- Brückenpfeiler und Stützmauern
- Treppenläufe und Rampen
Technik & Produktion
- Strömungskanäle mit trapezoidalem Querschnitt
- Werkzeugprofile und Schneidkanten
- Getriebezahnräder und Keilriemen
- Behälter und Trichterkonstruktionen
Das Trapez in der Geometrie
Das allgemeine Trapez ist ein Viereck mit einem Paar paralleler Seiten. Dieser universelle Rechner ermöglicht die Berechnung aller geometrischen Parameter basierend auf verschiedenen Eingabekombinationen. Die flexible Berechnungsmethode macht ihn zu einem wertvollen Werkzeug für technische und wissenschaftliche Anwendungen.
Die Berechnung erfolgt wahlweise über die Überstand-Methode (bei bekannter Höhe und horizontalem Versatz) oder über Winkel-Methoden (bei bekannten Winkeln und drei Seitenlängen). Alle Ergebnisse werden automatisch berechnet und umfassen Seitenlängen, Winkel, Fläche, Umfang, Diagonalen und Überstände.
Für spezialisierte Anwendungen stehen weitere Trapez-Rechner zur Verfügung, die auf bestimmte Trapez-Typen (symmetrisch, rechtwinklig) oder spezielle Berechnungen (nur Fläche, nur Winkel) optimiert sind.
|
|