Trapez Flächeninhalt berechnen
Rechner und Formeln zur Berechnung der Trapez-Fläche
Trapez Flächeninhalt Rechner
Trapez-Flächenberechnung
Der Flächeninhalt A eines Trapezes wird aus den parallelen Seiten a und c und der Höhe h berechnet. Die Formel basiert auf dem arithmetischen Mittel der Parallelseiten.
Trapez mit Flächenmarkierung
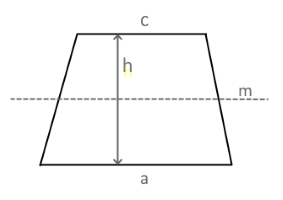
Das Diagramm zeigt ein Trapez mit den parallelen Seiten a und c sowie der Höhe h.
Die Fläche wird aus dem arithmetischen Mittel der Parallelseiten berechnet.
Flächenberechnung beim Trapez
Die Flächenberechnung beim Trapez basiert auf einer eleganten geometrischen Beziehung:
- Parallele Seiten: a und c sind die beiden parallelen Seiten
- Höhe h: Senkrechter Abstand zwischen den Parallelseiten
- Arithmetisches Mittel: (a+c)/2 ergibt die mittlere Breite
- Rechteck-Analogie: Fläche = mittlere Breite × Höhe
- Universelle Formel: Funktioniert für alle Trapez-Formen
- Grenzfälle: Bei a=c entsteht ein Rechteck
Herleitung der Trapez-Flächenformel
Die geometrische Herleitung verdeutlicht, warum die Formel funktioniert:
1. Verdopplung
- Trapez wird dupliziert
- Zweites Trapez um 180° gedreht
- Beide Trapeze zusammengefügt
- Parallelogramm mit doppelter Fläche entsteht
2. Rechteck-Umformung
- Schräge Seiten werden abgetrennt
- Umpositionierung zu einem Rechteck
- Rechteck: Länge = (a+c), Höhe = h
- Fläche = (a+c)×h, geteilt durch 2
Alternative: Mittellinie-Methode
Eine alternative Betrachtungsweise nutzt die Mittellinie des Trapezes:
Mittellinie m
Arithmetisches Mittel der parallelen Seiten
Vereinfachte Formel
Fläche = Mittellinie × Höhe
Praktische Anwendungen der Trapez-Flächenberechnung
Die Flächenberechnung von Trapezen ist in vielen Bereichen wichtig:
Bauwesen & Architektur
- Dachflächen mit trapezoidaler Form
- Grundstücks- und Raumflächen
- Fassadenelemente und Fenster
- Treppen und Rampen
Technik & Produktion
- Materialbedarfsberechnung
- Blechzuschnitte und Profile
- Kanäle und Rohrleitungen
- Maschinenbau-Komponenten
Landwirtschaft & Umwelt
- Ackerflächen und Parzellen
- Wasserflächen und Teiche
- Böschungen und Dämme
- Naturschutzgebiete
Wissenschaft & Forschung
- Numerische Integration (Trapezregel)
- Statistik und Datenanalyse
- Physikalische Messungen
- Geologische Untersuchungen
Formeln zur Trapez-Flächenberechnung
Hauptformel: Trapez-Flächeninhalt
Fläche aus parallelen Seiten a, c und Höhe h
Mittellinie m
Arithmetisches Mittel der Parallelseiten
Alternative Schreibweise
Fläche als Mittellinie mal Höhe
Spezialfall: Rechteck
Bei gleichen Parallelseiten wird es zum Rechteck
Herleitung über Rechteck
Geometrische Herleitung über Verdopplung
Herleitung Schritt für Schritt
Zweites Trapez um 180° drehen und anfügen
Ergebnis: Parallelogramm mit doppelter Fläche
Schräge Seiten abtrennen und umpositionieren
Ergebnis: Rechteck (a+c) × h
Rechteck-Fläche durch 2 teilen
Da das Rechteck doppelt so groß ist
\(A = \frac{(a+c) \cdot h}{2}\)
Universelle Trapez-Flächenformel
Visuelle Herleitung der Trapez-Flächenformel
Schritt 1: Verdopplung und Drehung
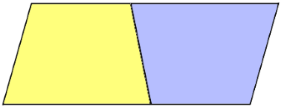
Das Trapez wird verdoppelt und das zweite um 180° gedreht angefügt.
Schritt 2: Umformung zum Rechteck
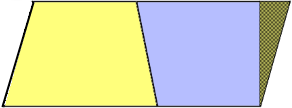
Schräge Seite wird abgetrennt...
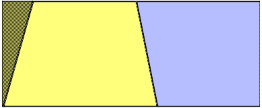
...und zur anderen Seite hinzugefügt.
Ergebnis der Herleitung
Das entstandene Rechteck hat die Länge (a+c) und die Höhe h. Da es die doppelte Fläche des ursprünglichen Trapezes hat, ergibt sich die Trapez-Fläche als: \[A_{Trapez} = \frac{A_{Rechteck}}{2} = \frac{(a+c) \cdot h}{2}\]
Rechenbeispiel
Gegeben
Gesucht: Flächeninhalt A des Trapezes
1. Mittellinie berechnen
Arithmetisches Mittel der Parallelseiten
2. Fläche berechnen (Methode 1)
Mit der Mittellinie
3. Fläche berechnen (Methode 2 - Hauptformel)
Direkte Anwendung der Hauptformel
4. Verifikation über Herleitung
\[A_{Rechteck} = (a + c) \cdot h = (3 + 5) \cdot 4 = 8 \cdot 4 = 32\]
Trapez-Fläche (Hälfte des Rechtecks):
\[A_{Trapez} = \frac{A_{Rechteck}}{2} = \frac{32}{2} = 16\]
Alle drei Methoden führen zum gleichen Ergebnis
Die Trapez-Flächenberechnung in Theorie und Praxis
Die Berechnung des Flächeninhalts eines Trapezes ist ein fundamentales Konzept der Geometrie, das weit über den mathematischen Unterricht hinausreicht. Die elegante Formel A = (a+c)·h/2 verbindet geometrische Intuition mit praktischer Anwendbarkeit und bildet die Grundlage für zahlreiche Berechnungen in Technik, Bauwesen und Naturwissenschaften.
Geometrische Grundlagen
Die Trapez-Flächenformel basiert auf fundamentalen geometrischen Prinzipien:
- Parallelität: Die beiden Seiten a und c sind parallel zueinander
- Höhe als Abstand: h ist der senkrechte Abstand zwischen den Parallelseiten
- Arithmetisches Mittel: (a+c)/2 repräsentiert die "mittlere Breite"
- Rechteck-Analogie: Das Trapez verhält sich flächenmäßig wie ein Rechteck mit der mittleren Breite
- Universalität: Die Formel gilt für alle Trapez-Varianten (gleichschenklig, rechtwinklig, allgemein)
Mathematische Eleganz der Herleitung
Die geometrische Herleitung der Formel zeigt die Schönheit mathematischen Denkens:
Verdopplungs-Methode
Durch Drehung und Zusammenfügung zweier identischer Trapeze entsteht ein Parallelogramm. Diese Methode verdeutlicht den Zusammenhang zur mittleren Breite.
Rechteck-Transformation
Die Umformung des Parallelogramms zum Rechteck zeigt, dass die Trapez-Fläche exakt der Hälfte eines entsprechenden Rechtecks entspricht.
Symmetrie-Eigenschaften
Die Formel spiegelt die Symmetrie-Eigenschaften des Trapezes wider und zeigt, warum die mittlere Breite als repräsentativ gelten kann.
Grenzfall-Betrachtungen
Bei a=c wird das Trapez zum Rechteck (A=a·h), bei c=0 zum Dreieck (A=a·h/2) - die Formel bleibt gültig.
Praktische Bedeutung und Anwendungen
Die Trapez-Flächenberechnung findet in zahlreichen praktischen Bereichen Anwendung:
Bauingenieurwesen
- Fundamentberechnung für trapezoidale Grundrisse
- Erdarbeiten und Böschungsberechnungen
- Dachflächen mit komplexer Geometrie
- Brücken- und Tunnelquerschnitte
Maschinenbau
- Materialbedarfsermittlung für Profile
- Querschnittsflächen von Bauteilen
- Strömungsquerschnitte in Kanälen
- Wärmetauscherflächen
Landwirtschaft und Umwelt
- Flächenberechnung für Ackerparzellen
- Wasserflächen und Bewässerungssysteme
- Naturschutzgebiete und Biotope
- Erosionsschutz und Böschungssicherung
Numerische Mathematik
- Trapezregel für numerische Integration
- Approximation von Kurvenintegralen
- Finite-Elemente-Methoden
- Statistische Flächenschätzungen
Moderne Entwicklungen und Technologien
In der digitalisierten Welt gewinnt die Trapez-Flächenberechnung neue Bedeutung:
- CAD-Systeme: Automatisierte Flächenberechnung in komplexen 3D-Modellen
- GIS-Anwendungen: Geografische Informationssysteme für Landvermessung
- Drohnen-Vermessung: Präzise Flächenbestimmung aus Luftbildern
- BIM-Technologie: Building Information Modeling für intelligente Gebäudeplanung
- Augmented Reality: Echtzeitberechnung von Flächen in AR-Anwendungen
- Maschinelles Lernen: Automatische Formerkennung und Flächenschätzung
Didaktische Aspekte
Die Trapez-Flächenberechnung eignet sich hervorragend als Lehrbeispiel:
Mathematische Konzepte
Verbindet geometrische Anschauung mit algebraischer Formelbildung und zeigt den Nutzen des arithmetischen Mittels.
Problemlösungsstrategien
Die Herleitung demonstriert kreative Problemlösungsansätze und zeigt, wie komplexe Formen auf einfachere reduziert werden können.
Praxisbezug
Bietet zahlreiche Anknüpfungspunkte an reale Anwendungen und motiviert zum Weiterlernen.
Visualisierung
Die graphische Herleitung unterstützt das Verständnis und macht abstrakte Konzepte greifbar.
Zusammenfassung
Die Trapez-Flächenberechnung ist mehr als nur eine geometrische Formel - sie ist ein Werkzeug, das Theorie und Praxis verbindet. Von der eleganten mathematischen Herleitung über vielfältige technische Anwendungen bis hin zu modernen digitalen Implementierungen zeigt sie die zeitlose Relevanz grundlegender geometrischer Konzepte. Die Formel A = (a+c)·h/2 steht exemplarisch für die Schönheit und Nützlichkeit mathematischen Denkens in einer technologisierten Welt.
|
|