Logit Funktion
Online Rechner und Formeln zur Logit Funktion - Umkehrfunktion der Sigmoid Funktion für Machine Learning
Logit Funktion Rechner
Logit (Log-Odds) Funktion
Die logit(p) oder Log-Odds Funktion ist die Umkehrfunktion der Sigmoid-Funktion und zentral im Machine Learning.
Logit Funktionskurve
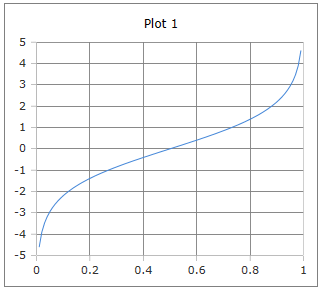
Kurve der Logit Funktion: Die Funktion bildet Wahrscheinlichkeiten (0,1) auf die reellen Zahlen (-∞,+∞) ab.
Eigenschaften: Streng monoton steigend, symmetrisch um (0.5, 0).
Formeln zur Logit Funktion
Grundformel
Logarithmus der Odds (Chancenverhältnis)
Alternative Form
Äquivalente Darstellung
Arctanh Form
Hyperbolische Darstellung
Umkehrfunktion
Sigmoid als Inverse der Logit-Funktion
Logistische Regression
Lineare Kombination der Prädiktoren im Logit-Raum
Eigenschaften
Spezielle Werte
Definitionsbereich
Offen zwischen 0 und 1 (exklusiv)
Wertebereich
Alle reellen Zahlen
Anwendung
Machine Learning, logistische Regression, Statistik und Datenanalyse.
Was sind Odds (Chancenverhältnis)?
Odds beschreiben das Verhältnis der Wahrscheinlichkeit für ein Ereignis zur Wahrscheinlichkeit gegen das Ereignis:
Beispiel: Bei einer Wahrscheinlichkeit von 75% (p = 0.75):
- Odds = 0.75 / 0.25 = 3
- Interpretation: "3 zu 1" oder "3:1"
- Log-Odds = ln(3) ≈ 1.099
Vorteile der Log-Odds:
- Symmetrisch um 0
- Unbegrenzter Wertebereich
- Linear in Regressionsmodellen
Ausführliche Beschreibung der Logit Funktion
Mathematische Definition
Die Logit-Funktion ist die Umkehrfunktion der Sigmoid-Funktion und transformiert Wahrscheinlichkeiten (0,1) in den gesamten reellen Zahlenbereich (-∞,+∞). Sie ist das Herzstück der logistischen Regression und vieler Machine Learning Algorithmen.
Verwendung des Rechners
Geben Sie eine Wahrscheinlichkeit zwischen 0 und 1 ein (exklusiv) und klicken Sie auf 'Rechnen'. Die Funktion ist nicht für p = 0 oder p = 1 definiert.
Historischer Hintergrund
Die Logit-Funktion wurde in den 1940er Jahren von Joseph Berkson eingeführt als Alternative zur Probit-Analyse. Der Name "Logit" ist eine Kontraktion von "Logistic Unit" und wurde schnell zum Standard in der Statistik.
Eigenschaften und Anwendungen
Machine Learning Anwendungen
- Logistische Regression (binäre Klassifikation)
- Neuronale Netze (Aktivierungsfunktion)
- Generalisierte lineare Modelle (GLM)
- Bayessche Statistik und MCMC
Statistische Anwendungen
- Epidemiologie (Krankheitsrisiko)
- Ökonometrie (Wahlverhalten)
- Psychometrie (Item Response Theory)
- Bioinformatik (Genexpression)
Besondere Eigenschaften
- Monotonie: Streng monoton steigend
- Symmetrie: logit(p) = -logit(1-p)
- Linearität: Ermöglicht lineare Modellierung
- Interpretierbarkeit: Koeffizienten als Log-Odds
Interessante Fakten
- Die Logit-Funktion ist die kanonische Link-Funktion für die Binomialverteilung
- Sie transformiert begrenzte Wahrscheinlichkeiten in unbegrenzte Log-Odds
- Zentral für die Maximum-Likelihood-Schätzung in der logistischen Regression
- Verwandt mit dem logistischen Wachstumsmodell in der Populationsdynamik
Berechnungsbeispiele
Beispiel 1
logit(0.5) = 0
Neutrale Wahrscheinlichkeit → Log-Odds = 0
Beispiel 2
logit(0.75) ≈ 1.099
75% Wahrscheinlichkeit → Odds 3:1
Beispiel 3
logit(0.25) ≈ -1.099
25% Wahrscheinlichkeit → Odds 1:3
Logistische Regression
Modellgleichung
In der logistischen Regression wird die Logit-Transformation verwendet:
Dies ermöglicht lineare Modellierung von Wahrscheinlichkeiten.
Interpretation
Die Koeffizienten βᵢ haben eine klare Interpretation:
- exp(βᵢ): Odds Ratio
- βᵢ > 0: Erhöht die Odds
- βᵢ < 0: Verringert die Odds
- βᵢ = 0: Kein Effekt
|
|