Softsign Funktion berechnen
Online Rechner und Formeln zur Softsign Funktion - Alternative zur Tanh Aktivierungsfunktion in neuronalen Netzen
Softsign Funktion Rechner
Softsign Aktivierungsfunktion
Die softsign(x) oder Softsign-Funktion ist eine sanfte Alternative zur Tanh-Funktion als Aktivierungsfunktion in neuronalen Netzen.
Sanfte S-förmige Kurve
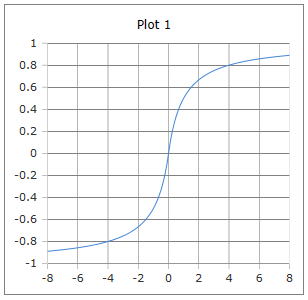
Die Kurve der Softsign Funktion: Sanfte S-Form mit Werten zwischen -1 und +1.
Eigenschaften: Glatt, monoton steigend, langsamer sättigend als Tanh.
Warum ist Softsign eine sanfte Alternative?
Die Softsign-Funktion bietet mehrere Vorteile gegenüber anderen Aktivierungsfunktionen:
- Langsame Sättigung: Weniger aggressive Asymptoten als Tanh
- Einfache Berechnung: Nur Division und Absolutwert
- Symmetrie: Punktsymmetrisch um den Ursprung
- Begrenzte Ausgabe: Werte zwischen -1 und +1
- Null-zentriert: Ausgabe um 0 zentriert
- Monotonie: Streng monoton steigend
Vergleich: Softsign vs. Tanh
Beide Funktionen haben S-förmige Kurven mit Werten zwischen -1 und +1, aber unterschiedliche Eigenschaften:
Softsign: x/(1+|x|)
- Langsame Sättigung bei großen |x|
- Computationally weniger aufwendig
- Linearer Verlauf um x = 0
- Weniger vanishing gradients
Tanh: (e^x - e^(-x))/(e^x + e^(-x))
- Schnelle Sättigung bei großen |x|
- Exponentialfunktionen erforderlich
- S-förmiger Verlauf um x = 0
- Stärkere vanishing gradients
Formeln zur Softsign Funktion
Grundformel
Einfache rationale Funktion
Ableitung
Immer positiv
Stückweise Definition
Aufgeteilte Darstellung
Umkehrfunktion
Für |y| < 1
Grenzwerte
Horizontale Asymptoten
Symmetrie
Ungerade Funktion
Eigenschaften
Spezielle Werte
Definitionsbereich
Alle reellen Zahlen
Wertebereich
Zwischen -1 und +1
Anwendung
Neuronale Netze, Deep Learning, alternative Aktivierungsfunktion, sanfte Normalisierung.
Ausführliche Beschreibung der Softsign Funktion
Mathematische Definition
Die Softsign-Funktion ist eine sanfte, S-förmige Funktion, die als Alternative zur hyperbolischen Tangens-Funktion entwickelt wurde. Sie bietet ähnliche Eigenschaften wie Tanh, ist aber computational günstiger und zeigt ein anderes Sättigungsverhalten.
Verwendung des Rechners
Geben Sie eine beliebige reelle Zahl ein und klicken Sie auf 'Rechnen'. Die Funktion ist für alle reellen Zahlen definiert und liefert Werte zwischen -1 und +1.
Historischer Hintergrund
Die Softsign-Funktion wurde als Teil der Suche nach besseren Aktivierungsfunktionen für neuronale Netze entwickelt. Sie wurde besonders in den frühen 2000er Jahren als computationally effiziente Alternative zu Tanh vorgeschlagen.
Eigenschaften und Anwendungen
Machine Learning Anwendungen
- Aktivierungsfunktion in neuronalen Netzen
- Alternative zu Tanh in versteckten Schichten
- Sanfte Normalisierung von Eingabewerten
- Regularisierung durch langsamere Sättigung
Computational Vorteile
- Keine Exponentialfunktionen erforderlich
- Einfache Ableitung für Backpropagation
- Numerisch stabil für alle Eingabewerte
- Geringerer Rechenaufwand als Tanh
Mathematische Eigenschaften
- Monotonie: Streng monoton steigend
- Symmetrie: Ungerade Funktion (punktsymmetrisch)
- Differenzierbarkeit: Überall differenzierbar außer bei x = 0
- Sättigung: Langsame Annäherung an ±1
Interessante Fakten
- Die Ableitung softsign'(x) = 1/(1+|x|)² ist immer positiv
- Softsign sättigt langsamer als Tanh, was weniger vanishing gradients bedeutet
- Die Funktion ist bei x = 0 nicht differenzierbar (aber stetig)
- Computational cost ist deutlich geringer als bei Sigmoid oder Tanh
Berechnungsbeispiele
Beispiel 1
softsign(0) = 0
Neutrale Eingabe → Nullausgang
Beispiel 2
softsign(1) = 0.5
Positive Eingabe → Positive Aktivierung
Beispiel 3
softsign(-3) = -0.75
Negative Eingabe → Negative Aktivierung
Vergleich mit anderen Aktivierungsfunktionen
vs. Tanh
Softsign vs. hyperbolische Tangens:
- Ähnlicher Wertebereich (-1, 1)
- Langsamere Sättigung
- Geringere Rechenkosten
- Weniger vanishing gradients
vs. Sigmoid
Softsign vs. Sigmoid-Funktion:
- Symmetrisch um Null (vs. 0-1 Range)
- Null-zentrierte Ausgabe
- Bessere Konvergenzeigenschaften
- Einfachere Berechnung
vs. ReLU
Softsign vs. Rectified Linear Unit:
- Begrenzte Ausgabe (vs. unbegrenzt)
- Glatte Funktion (vs. nicht-differenzierbar)
- Beide Richtungen aktiv
- Komplexere Berechnung
Vor- und Nachteile
Vorteile
- Computationally effizient (keine Exponentialfunktionen)
- Null-zentrierte Ausgabe verbessert Konvergenz
- Langsamere Sättigung reduziert vanishing gradients
- Numerisch stabil für alle Eingabewerte
- Einfache Implementierung
Nachteile
- Nicht differenzierbar bei x = 0 (praktisch meist vernachlässigbar)
- Langsamer als ReLU-basierte Funktionen
- Weniger verbreitet als Sigmoid/Tanh
- Kann bei sehr großen Netzen trotzdem sättigen
- Begrenzte empirische Studien im Vergleich zu ReLU
|
|