Widerstand Parallelschaltung für 2 Widerstände
Rechner und Formel zur Berechnung zweier Widerstände einer Parallelschaltung
2-Widerstand Parallelschaltung
Berechnungsmodi
Berechnen Sie entweder den Gesamtwiderstand aus zwei bekannten Widerständen oder einen unbekannten Parallelwiderstand R₂.
2-Widerstand Parallelschaltung
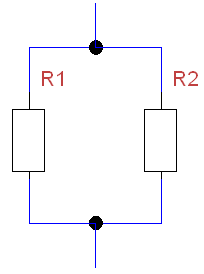
Schaltbild: Parallelschaltung zweier Widerstände
Zwei Berechnungsmodi
- Gesamtwiderstand berechnen: Aus R₁ und R₂ → Rges
- Parallelwiderstand R₂ berechnen: Aus R₁ und Rges → R₂
Produktformel
Spezialfall
Formeln zur Parallelschaltung zweier Widerstände
1. Gesamtwiderstand berechnen
Produktformel für zwei Widerstände:
2. Parallelwiderstand R₂ berechnen
Umgestellte Produktformel:
3. Herleitung über Leitwerte
Die Produktformel kann auch über Leitwerte (G = 1/R) hergeleitet werden:
Praktische Rechenbeispiele
Beispiel 1: Gesamtwiderstand berechnen
Gegeben: R₁ = 30Ω, R₂ = 20Ω
✓ Kontrolle: 12Ω < 20Ω (kleinster Widerstand)
Beispiel 2: Parallelwiderstand R₂ berechnen
Gegeben: R₁ = 100Ω, Rges = 30Ω
✓ Kontrolle: 30Ω < 43Ω < 100Ω
Beispiel 3: Gleiche Widerstände (Spezialfall)
Spezialfall: Wenn beide Widerstände gleich groß sind (R₁ = R₂ = R):
Merksatz: Bei zwei gleichen Widerständen in Parallelschaltung halbiert sich der Widerstandswert.
Stromverteilung und praktische Anwendungen
Stromaufteilung
In einer Parallelschaltung teilt sich der Gesamtstrom umgekehrt proportional zu den Widerstandswerten auf. Durch den kleineren Widerstand fließt der größere Strom.
Stromverteilungsformeln
Praktische Anwendungen
- Widerstandswerte verringern: Reduktion des Gesamtwiderstands
- Shunt-Widerstände: Strommessung durch Parallelwiderstände
- LED-Schaltungen: Vorwiderstände für parallele LED-Stränge
- Bias-Schaltungen: Arbeitspunkteinstellung in Verstärkern
- Spannungsteiler-Belastung: Auswirkungen von Lastströmen
Wichtige Hinweise
- Rges ist immer kleiner als der kleinste Einzelwiderstand
- Die Gesamtleistung steigt (Pges = P₁ + P₂)
- Unterschiedliche Ströme bei verschiedenen Widerständen
- Belastbarkeit der Widerstände beachten
Merksätze
- Bei gleichen Widerständen: Rges = R/2
- Größerer Strom durch kleineren Widerstand
- Gleiche Spannung an beiden Widerständen
- Produktformel nur für zwei Widerstände
|
|