Widerstand Parallelschaltung
Rechner und Formeln zur Berechnung parallelgeschalteter Widerstände
Parallelwiderstand Rechner
Eingabeformat
Geben Sie die Widerstandswerte durch Semikolon getrennt ein.
Beispiel: 100; 220; 470
Parallelschaltung
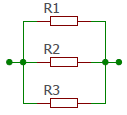
Parallelschaltung von Widerständen
Eigenschaften
- Gleiche Spannung an allen Widerständen
- Gesamtstrom ist die Summe der Teilströme
- Gesamtwiderstand ist immer kleiner als der kleinste Einzelwiderstand
Grundformel
Spezialfälle
Formeln zur Parallelschaltung
Allgemeine Formel
Für n Widerstände:
Produktformel (2 Widerstände)
Vereinfachte Formel für zwei Widerstände:
Gleiche Widerstände
Wenn alle n Widerstände gleich sind:
Praktische Beispiele
Beispiel 1: Drei verschiedene Widerstände
Gegeben: R₁ = 4Ω, R₂ = 6Ω, R₃ = 12Ω
✓ Kontrolle: 2Ω < 4Ω (kleinster Widerstand)
Beispiel 2: Zwei gleiche Widerstände
Gegeben: Zwei 100Ω-Widerstände parallel
Bei gleichen Widerständen: Rges = R/n
Beispiel 3: Praktische Anwendung - Widerstand reduzieren
Aufgabe: Ein 470Ω-Widerstand soll auf etwa 150Ω reduziert werden. Welcher Widerstand muss parallel geschaltet werden?
Stromverteilung und Anwendungen
Stromverteilung in der Parallelschaltung
In einer Parallelschaltung teilt sich der Gesamtstrom umgekehrt proportional zu den Widerstandswerten auf. Der Strom fließt bevorzugt durch den kleineren Widerstand.
Stromverteilungsformel
Häufige Anwendungen
- Elektrische Beleuchtung: Lampen in Hausinstallationen
- Elektronik: Spannungsteiler und Bias-Schaltungen
- Messtechnik: Shunt-Widerstände für Strommessung
- Leistungsanpassung: Verringerung des Gesamtwiderstands
Wichtiger Hinweis
Bei der Parallelschaltung von Widerständen erhöht sich die Gesamtleistung, da mehr Strom fließt.
Beachten Sie: Belastbarkeit der Spannungsquelle und thermische Belastung der Bauteile!
Merksätze
- Rges ist immer kleiner als der kleinste Einzelwiderstand
- Durch kleine Widerstände fließt mehr Strom
- Alle Widerstände haben die gleiche Spannung
- Die Gesamtleistung ist die Summe der Einzelleistungen
Eingabehinweise für den Rechner
Korrekte Eingabe
- Format: Werte durch Semikolon trennen (z.B. 100; 220; 470)
- Einheiten: Alle Werte in der gleichen Einheit eingeben
- Dezimalzeichen: Komma (,) oder Punkt (.) verwenden
- Exponenten: Nicht erlaubt - verwenden Sie 1000 statt 1E3
- Ergebnis: Wird in der gleichen Einheit wie die Eingabe angezeigt
|
|