RL Tiefpass berechnen
Rechner und Formeln zur Berechnung der Parameter eines RL Tiefpasses
RL Tiefpass Rechner
RL Tiefpass
Diese Funktion berechnet die Eigenschaften eines Tiefpasses aus Widerstand und Spule. Es wird bei der gegebenen Frequenz die Ausgangsspannung, Dämpfung und die Phasendrehung berechnet.
Schaltungsdiagramm & Parameter
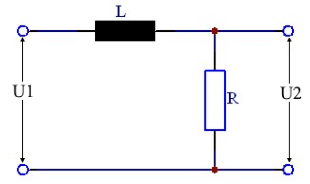
Parameter
Beispielrechnungen
Praktische Rechenbeispiele
Beispiel 1: Audio-Tiefpass
Gegeben: R = 8Ω, L = 1mH, f = 3kHz, U₁ = 10V
Beispiel 2: Grenzfrequenz-Berechnung
Gegeben: R = 100Ω, L = 10mH
Beispiel 3: Phasenverschiebung
Gegeben: R = 50Ω, L = 5mH, f = 1kHz
Tiefpass-Eigenschaften
Frequenzverhalten:
Phasenverhalten:
Formeln zum RL Tiefpass
Spannungsverhältnis berechnen
Die Ausgangspannung U2 eines RL Tiefpass wird nach der folgenden Formel berechnet.
Ausgangsspannung
oder einfacher, wenn XL bekannt ist:
Blindwiderstand
Der induktive Blindwiderstand steigt proportional zur Frequenz.
Dämpfung in Dezibel
Die Dämpfung beträgt bei der Grenzfrequenz 3dB. Sie kann für die verschiedenen Frequenzen nach den Formeln unten berechnet werden.
Dämpfung (einfach)
Wenn Ein- und Ausgangsspannung bekannt sind.
Dämpfung (komplex)
Direktberechnung aus R, L und ω.
Phasenverschiebung
In einem RL Tiefpass eilt die Ausgangsspannung der Eingangsspannung, je nach Frequenz um 0° bis -90° nach. Bei der Grenzfrequenz beträgt die Phasenverschiebung -45°.
Phasenwinkel (einfach)
Phasenwinkel (komplex)
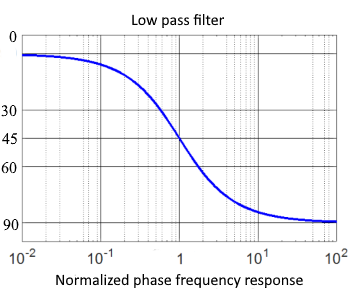
Grenzfrequenz
Bei Grenzfrequenz fg ist der Wert des Amplituden-Frequenzganges gleich 0,707. Das entspricht –3dB.
Grenzfrequenz-Formeln
Praktische Anwendungen
Audio-Technik
- Subwoofer-Filter
- Crossover-Netzwerke
- Rauschfilter
- Anti-Aliasing
Signalverarbeitung
- Glättungsfilter
- Integrator
- Entstörung
- EMV-Filter
Leistungselektronik
- Motordrosseln
- Netzfilter
- Gleichrichterschaltungen
- Schaltnetzteile