RL Parallelschaltung berechnen
Rechner und Formeln zur Berechnung der Parameter einer RL Parallelschaltung
RL Parallelschaltung Rechner
RL Parallelschaltung
Der Rechner berechnet Strom, Leistungen, Schein- und Blindwiderstand in der Parallelschaltung eines Widerstands und einer Spule. Geben Sie die Werte für Spule, Widerstand, Frequenz und Spannung ein.
Schaltungsdiagramm & Parameter
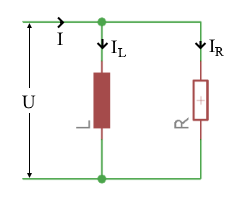
Parameter Legende
| I | Gesamtstrom |
| IR | Strom durch den Widerstand |
| IL | Strom durch die Spule |
| XL | Induktiver Blindwiderstand |
| Z | Impedanz (Gesamtwiderstand) |
| Y | Admittanz (Scheinleitwert) |
| P | Wirkleistung |
| Q | Blindleistung |
| S | Scheinleistung |
| φ | Phasenwinkel |
Beispielrechnungen
Praktische Rechenbeispiele
Beispiel 1: Niederfrequenz
Gegeben: L = 100 mH, R = 100 Ω, f = 50 Hz, U = 230 V
Beispiel 2: Audiofrequenz
Gegeben: L = 10 mH, R = 8 Ω, f = 1 kHz, U = 12 V
Beispiel 3: Hochfrequenz
Gegeben: L = 1 µH, R = 50 Ω, f = 100 MHz, U = 5 V
Wichtige Umrechnungen
Frequenzeinheiten:
Leistungseinheiten:
RL Parallelschaltung - Theorie und Formeln
Was ist eine RL Parallelschaltung?
Bei einer RL-Parallelschaltung sind ein ohmscher Widerstand R und eine Induktivität L parallel geschaltet. An beiden Bauteilen liegt die gleiche Spannung an, aber der Strom verteilt sich entsprechend den jeweiligen Widerstandswerten. Der Gesamtstrom ist die geometrische Summe der Teilströme.
Berechnungsformeln
Stromdreieck
Gesamtstrom
Geometrische Addition der Teilströme
Wirkstrom
Strom durch den ohmschen Widerstand
Blindstrom
Strom durch die Induktivität
Phasenwinkel
Phasenverschiebung zwischen U und I
Leitwertdreieck
Bei Parallelschaltungen ist es oft einfacher, mit Leitwerten zu rechnen:
Admittanz
Gesamtleitwert der Schaltung
Konduktanz
Wirkleitwert (Kehrwert des Widerstands)
Suszeptanz
Blindleitwert der Induktivität
Impedanz (Gesamtwiderstand)
Gesamtimpedanz
Parallelschaltung von R und L
Blindwiderstand
Frequenzabhängiger Blindwiderstand
Leistungsdreieck
Scheinleistung
Gesamtleistung der Schaltung
Wirkleistung
Nutzbare Leistung im Widerstand
Blindleistung
Pendelleistung in der Induktivität
Leistungsfaktor
Verhältnis Wirk- zu Scheinleistung
Praktische Anwendungen
Filter & Frequenzweichen:
Motorschaltungen:
Messtechnik:
Verhalten bei verschiedenen Frequenzen
Frequenzabhängiges Verhalten
- Niedrige Frequenzen (f → 0): XL → 0, Spule wirkt wie Kurzschluss
- Mittlere Frequenzen: XL ≈ R, beide Zweige tragen zum Strom bei
- Hohe Frequenzen (f → ∞): XL → ∞, Widerstand dominiert
- Resonanz: Tritt bei RL-Parallelschaltungen nicht auf (nur bei RLC)
- Zeitkonstante: τ = L/R bestimmt Einschwingverhalten
Design-Hinweise
Wichtige Designaspekte
- Stromaufteilung: Bei niedrigen Frequenzen fließt mehr Strom durch die Spule
- Verluste: Nur im Widerstand entstehen Verlustleistungen
- Phasenwinkel: Strom eilt der Spannung vor (induktiv)
- Blindleistung: Spule speichert und gibt Energie zurück
- Spannungsqualität: Parallelschaltung verbessert Leistungsfaktor
- Kurzschlussverhalten: Spule begrenzt Stromänderung