}

RL Reihenschaltung berechnen

Rechner und Formeln zur Berechnung einer RL Reihenschaltung

RL Reihenschaltung Rechner

RL Reihenschaltung

Der Rechner berechnet zu einer Reihenschaltung aus einem Widerstand und einer Spule die Spannungen, Leistungen, den Strom, Schein- und Blindwiderstand. Geben Sie die Werte für Spule, Widerstand, Frequenz und Spannung ein.

Spule L

Widerstand R

Frequenz f

Spannung U

Dezimalstellen

Ergebnisse

Blindwiderstand X_L:

Gesamtwiderstand Z:

Spannung U_R:

Spannung U_L:

Strom I:

Wirkleistung P:

Blindleistung Q:

Scheinleistung S:

Phasenwinkel φ:

Schaltungsdiagramm & Parameter

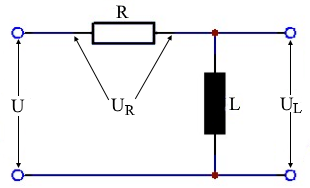
Parameter Legende

U	Angelegte Spannung
U_R	Spannung am Widerstand
U_L	Spannung an der Spule
I	Strom
R	Ohmscher Widerstand
X_L	Induktiver Blindwiderstand
Z	Scheinwiderstand - Impedanz
P	Wirkleistung
Q	Induktive Blindleistung
S	Scheinleistung
φ	Phasenverschiebung in °

Beispielrechnungen

Praktische Rechenbeispiele

Beispiel 1: Niederfrequenz Motor

Gegeben: L = 50 mH, R = 10 Ω, f = 50 Hz, U = 230 V

\[X_L = 2\pi f L = 2\pi \cdot 50 \cdot 0{,}05 = 15{,}7 \text{ Ω}\]

\[Z = \sqrt{R^2 + X_L^2} = \sqrt{10^2 + 15{,}7^2} = 18{,}7 \text{ Ω}\]

\[I = \frac{U}{Z} = \frac{230}{18{,}7} = 12{,}3 \text{ A}\]

\[U_R = I \cdot R = 12{,}3 \cdot 10 = 123 \text{ V}\]

\[U_L = I \cdot X_L = 12{,}3 \cdot 15{,}7 = 193 \text{ V}\]

Motor-Anlaufschaltung

Beispiel 2: Audio-Frequenzweiche

Gegeben: L = 1 mH, R = 4 Ω, f = 3 kHz, U = 12 V

\[X_L = 2\pi \cdot 3000 \cdot 0{,}001 = 18{,}8 \text{ Ω}\]

\[Z = \sqrt{4^2 + 18{,}8^2} = 19{,}2 \text{ Ω}\]

\[I = \frac{12}{19{,}2} = 0{,}625 \text{ A}\]

\[φ = \arctan\left(\frac{18{,}8}{4}\right) = 78{,}0°\]

\[P = I^2 \cdot R = 0{,}625^2 \cdot 4 = 1{,}56 \text{ W}\]

Hochpass-Verhalten

Beispiel 3: HF-Schaltung

Gegeben: L = 10 µH, R = 50 Ω, f = 10 MHz, U = 5 V

\[X_L = 2\pi \cdot 10 \times 10^6 \cdot 10 \times 10^{-6} = 628 \text{ Ω}\]

\[Z = \sqrt{50^2 + 628^2} = 630 \text{ Ω}\]

\[I = \frac{5}{630} = 7{,}94 \text{ mA}\]

\[U_R = 7{,}94 \times 10^{-3} \cdot 50 = 0{,}4 \text{ V}\]

\[U_L = 7{,}94 \times 10^{-3} \cdot 628 = 4{,}99 \text{ V}\]

Spule dominiert bei HF

Wichtige Umrechnungen

Induktivitätseinheiten:

1 H = 1.000 mH

1 mH = 1.000 µH

1 µH = 1.000 nH

1 nH = 0,001 µH

Spannungseinheiten:

1 kV = 1.000 V

1 V = 1.000 mV

1 mV = 1.000 µV

1 µV = 0,001 mV

RL Reihenschaltung - Theorie und Formeln

Was ist eine RL Reihenschaltung?

Bei einer RL-Reihenschaltung sind ein ohmscher Widerstand R und eine Induktivität L in Serie geschaltet. Durch beide Bauteile fließt der gleiche Strom, aber die Spannung verteilt sich entsprechend den jeweiligen Widerstandswerten. Die Gesamtspannung ist die geometrische Summe der Teilspannungen.

Berechnungsformeln

Spannungsdreieck

Gesamtspannung

\[U = \sqrt{U_R^2 + U_L^2}\]

Geometrische Addition der Teilspannungen

Wirkspannung

\[U_R = I \cdot R = U \cdot \cos(φ)\]

Spannung am ohmschen Widerstand

Blindspannung

\[U_L = I \cdot X_L = U \cdot \sin(φ)\]

Spannung an der Induktivität

Strom

\[I = \frac{U}{Z} = \frac{U}{\sqrt{R^2 + X_L^2}}\]

Strom ist überall gleich

Widerstandsdreieck

Gesamtimpedanz

\[Z = \sqrt{R^2 + X_L^2} = \frac{U}{I}\]

Scheinwiderstand der Schaltung

Wirkwiderstand

\[R = \sqrt{Z^2 - X_L^2} = Z \cdot \cos(φ)\]

Ohmscher Widerstand

Blindwiderstand

\[X_L = 2\pi f L = Z \cdot \sin(φ)\]

Frequenzabhängiger Blindwiderstand

Phasenwinkel

\[φ = \arctan\left(\frac{X_L}{R}\right)\]

Phasenverschiebung zwischen U und I

Leistungsdreieck

Scheinleistung

\[S = \sqrt{P^2 + Q^2} = U \cdot I\]

Gesamtleistung der Schaltung

Wirkleistung

\[P = U_R \cdot I = I^2 \cdot R\]

Nutzbare Leistung (nur im Widerstand)

Blindleistung

\[Q = U_L \cdot I = I^2 \cdot X_L\]

Pendelleistung in der Induktivität

Leistungsfaktor

\[\cos(φ) = \frac{P}{S} = \frac{R}{Z}\]

Verhältnis Wirk- zu Scheinleistung

Phasenbeziehungen

Spannungsphasen

\[φ = \arctan\left(\frac{U_L}{U_R}\right)\]

Phasenwinkel aus Spannungen

Widerstandsphasen

\[φ = \arctan\left(\frac{X_L}{R}\right)\]

Phasenwinkel aus Widerständen

Phasenverhalten

φ > 0°: Induktives Verhalten - Strom eilt Spannung nach
φ = 0°: Rein ohmsches Verhalten - Strom und Spannung in Phase
φ = 90°: Rein induktives Verhalten - Strom eilt 90° nach
Typisch: 0° < φ < 90° bei RL-Schaltungen

Praktische Anwendungen

Motoren & Antriebe:

• Anlaufschaltungen

• Strombegrenzung

• Drosseln

• Transformatoren

Filter & Weichen:

• Hochpass-Filter

• Frequenzweichen

• Entstörfilter

• Audio-Crossover

HF-Technik:

• Antennentuner

• Impedanzanpassung

• Oszillatoren

• Schwingkreise

Verhalten bei verschiedenen Frequenzen

Frequenzabhängiges Verhalten

Niedrige Frequenzen (f → 0): X_L → 0, Widerstand dominiert
Mittlere Frequenzen: X_L ≈ R, beide Komponenten wichtig
Hohe Frequenzen (f → ∞): X_L → ∞, Spule dominiert
Grenzfrequenz: f_g = R/(2πL) wenn X_L = R
Hochpass-Verhalten: Niedrige Frequenzen werden gedämpft

Design-Hinweise

Wichtige Designaspekte

Spannungsaufteilung: U_L kann größer als U_ges sein!
Verluste: Nur im Widerstand entstehen Verlustleistungen
Phasenwinkel: Strom eilt der Spannung nach (induktiv)
Resonanz: Keine Resonanz bei RL-Schaltungen
Zeitkonstante: τ = L/R bestimmt Einschwingverhalten
Selbstinduktion: Spule erzeugt Spannungsspitzen beim Schalten

Weitere Induktions Rechner

Induktivität • Blindwiderstand einer Spule • RL Reihenschaltung berechnen • RL Parallelschaltung berechnen • RL Hochpass-berechnen • RL Tiefpass berechnen • RL Grenzfrequenz berechnen • RL Differenzierglied berechnen • Transformator berechnen