RL Differenzierer berechnen
Rechner und Formeln zur Berechnung eines RL Differenzierglieds
RL Differenzierer Rechner
RL Differenzierglied
Mit dieser Funktion können die Eigenschaften eines Differenzierglieds aus einem Widerstand und einer Spule berechnet werden. Die Funktion berechnet die Spule, den Widerstand oder die Periodendauer bzw. die Frequenz.
Schaltungsdiagramm & Signale
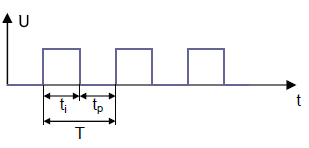
T = Periode, t1 = Impuls
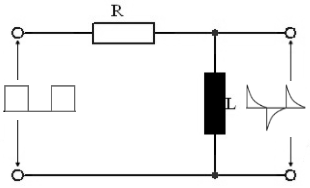
Funktionsweise
Das Differenzierglied funktioniert als Impulsformerstufe. Das RL-Glied erzeugt aus einer Rechteckspannung am Eingang eine impulsartige Wechselspannung am Ausgang der Schaltung.
Zeitkonstante
τ (Tau) bestimmt das Zeitverhalten des Differenzierers.
Beispielrechnungen
Praktische Rechenbeispiele
Beispiel 1: Audio-Impulsgenerator
Gegeben: L = 10 mH, R = 100 Ω, Impulsbreite t1 = 1 ms
Beispiel 2: Digitale Flanken-Detektion
Gegeben: L = 1 µH, Impulsbreite t1 = 100 ns, τ = 20 ns
Beispiel 3: HF-Impulsgenerator
Gegeben: R = 50 Ω, t1 = 10 ns, τ = 2 ns
Optimale Verhältnisse
Impulslänge zu Zeitkonstante:
Typische Anwendungen:
RL Differenzierer - Theorie und Formeln
Was ist ein RL Differenzierer?
Ein RL-Differenzierer ist eine Impulsformerschaltung, die aus Rechteckimpulsen kurze, nadelförmige Impulse erzeugt. Das Ausgangssignal entspricht näherungsweise der mathematischen Ableitung des Eingangssignals. Die Zeitkonstante τ = L/R bestimmt die Eigenschaften der Impulsformung.
Berechnungsformeln
Zeitkonstante und Grundformeln
Zeitkonstante
Bestimmt das Zeitverhalten der Schaltung
Widerstand berechnen
Widerstand für gewünschte Zeitkonstante
Induktivität berechnen
Induktivität für gewünschte Zeitkonstante
Übertragungsfunktion
Laplace-Übertragungsfunktion
Impulsverhältnisse für optimale Differenzierung
5τ-Regel
Grundregel für gute Differenzierung
10τ-Regel
Optimale Differenzierung mit kurzen Impulsen
Universelle Formel
n = 5 für grundlegende, n = 10 für optimale Differenzierung
Signalverhalten und Ausgangskenngrößen
Impulsbreite (Ausgang)
Breite der Ausgangsnadelimpulse
Amplitude (relativ)
Höhe der Ausgangsnadelimpulse
Impulsverhalten
- Positive Flanke: Positiver Ausgangsnadelimpuls
- Negative Flanke: Negativer Ausgangsnadelimpuls
- Konstante Spannung: Kein Ausgangssignal
- Impulsdauer: Etwa 2-3 Zeitkonstanten
Design-Regeln und Optimierung
Spulenauswahl
- Niedrige Frequenzen: mH-Bereich
- Audio/Digital: µH-Bereich
- HF/Impuls: nH-Bereich
- Güte: Möglichst hohe Güte verwenden
Widerstandsauswahl
- Impedanzanpassung: An Quelle/Last anpassen
- Bandbreite: Kleinerer R = größere Bandbreite
- Rauschen: Kompromiss zwischen R und Bandbreite
- Belastbarkeit: Ausreichende Leistung
Praktische Anwendungen
Signal-Processing:
HF-Technik:
Digitaltechnik:
Design-Hinweise
Wichtige Designaspekte
- Zeitkonstante: τ sollte 5-10 mal kleiner als Impulsbreite sein
- Bandbreite: f₃dB ≈ 1/(2πτ) - begrenzt die maximale Arbeitsfrequenz
- Impedanzanpassung: R sollte zur Systemimpedanz passen
- Parasitäre Effekte: Spulen-Eigenkapazität bei hohen Frequenzen beachten
- Sättigung: Spulenkern darf bei großen Strömen nicht sättigen
- Temperatur: Temperaturdrift von L und R berücksichtigen
Signalverhalten
Charakteristische Eigenschaften
- Eingangssignal: Rechteckimpulse mit definierten Flanken
- Ausgangssignal: Kurze Nadelimpulse bei jeder Flanke
- Positive Flanke: Positiver Ausgangsnadelimpuls
- Negative Flanke: Negativer Ausgangsnadelimpuls
- Impulsdauer: Etwa 2,2 Zeitkonstanten (10%-90% Kriterium)
- Amplitude: Abhängig vom Verhältnis τ/t₁