Frequenz und Periode

Rechner und Formeln zur Berechnung von Frequenz und Periode von Wechselspannungen

Periode und Frequenz Rechner

Frequenz-Perioden-Rechner

Auf dieser Seite können Sie die Dauer der Periode zu einer bestimmten Frequenz, oder die Frequenz zu einer Periode berechnen.

Was soll berechnet werden?
 
 
Ergebnis
Periodendauer:
Frequenz:

Frequenz & Periodendauer

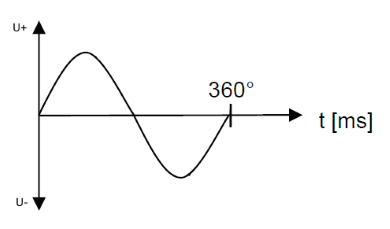
Eine Periode einer Sinusschwingung

Eine Periode einer Sinusschwingung

Parameter
\(\displaystyle f\) = Frequenz [Hz]
\(\displaystyle T\) = Periodendauer [s]
\(\displaystyle \omega = 2\pi f\) = Kreisfrequenz [rad/s]
Grundformeln
\[f = \frac{1}{T}\]
\[T = \frac{1}{f}\]
Tipp

Einen Rechner zur Berechnung von Frequenz und Wellenlängen finden Sie hier.

Beispielrechnungen

Praktische Rechenbeispiele

Beispiel 1: Netzfrequenz

Gegeben: f = 50Hz (europäische Netzfrequenz)

\[T = \frac{1}{50Hz} = 0{,}02s = 20ms\]
Eine Netzperiode dauert 20 Millisekunden
Beispiel 2: Audio-Frequenz

Gegeben: T = 0,1s (Periodendauer)

\[f = \frac{1}{0{,}1s} = 10Hz\]
Tieffrequente Audioschwingung
Beispiel 3: Hochfrequenz

Gegeben: f = 2,4GHz (WLAN-Frequenz)

\[T = \frac{1}{2{,}4 \times 10^9Hz} = 4{,}17 \times 10^{-10}s = 0{,}417ns\]
Extrem kurze Periodenzeiten bei Mikrowellen
Frequenzbereiche und typische Anwendungen
Niederfrequenz (NF):
Bereich: 20Hz - 20kHz
Periode: 50ms - 50µs
Anwendung: Audio, Hörbereich
Hochfrequenz (HF):
Bereich: 3MHz - 30MHz
Periode: 333ns - 33ns
Anwendung: Kurzwelle, Funk
Mikrowellen:
Bereich: 300MHz - 300GHz
Periode: 3,3ns - 3,3ps
Anwendung: WLAN, Mobilfunk

Verhältnis von Frequenz und Periode

Grundlagen

Die Frequenz ist der Kehrwert der Periodendauer, also die Anzahl der Schwingungen pro Sekunde. Die Einheit der Frequenz ist Hertz (Hz), die Einheit der Periodendauer ist Sekunde (s). Die Periode ist die Zeit, die eine Schwingung dauert. Die Periode kann auch als Winkelmaß angegeben werden, z.B. 360° für eine Sinusschwingung.

Formeln zur Frequenz und Periodenzeit

Die Frequenz ist die Anzahl der Perioden pro Sekunde. Zur Berechnung der Frequenz gilt daher die Formel:

Frequenz-Formel
\[f = \frac{1}{T}\]

Die Frequenz ist der Kehrwert der Periodendauer.

Die Dauer einer Periode wird mit der folgenden Formel berechnet:

Perioden-Formel
\[T = \frac{1}{f}\]

Die Periodendauer ist der Kehrwert der Frequenz.

Erweiterte Beziehungen

Kreisfrequenz
\[\omega = 2\pi f = \frac{2\pi}{T}\]

Kreisfrequenz in Radiant pro Sekunde [rad/s]

Wellenzahl
\[k = \frac{2\pi}{\lambda} = \frac{\omega}{c}\]

Wellenzahl bei Ausbreitung mit Geschwindigkeit c

Praktische Anwendungen

Elektrotechnik
  • Netzfrequenz (50/60Hz)
  • Taktfrequenzen
  • Schwingkreise
  • Filter-Design
Kommunikation
  • Trägerfrequenzen
  • Modulationsfrequenzen
  • Baudrate/Bitrate
  • Kanaltrennung
Messtechnik
  • Abtastfrequenz
  • Zeitbasis
  • Synchronisation
  • Spektralanalyse

Einheiten und Größenordnungen

Häufig verwendete Einheiten
Frequenz-Einheiten:
Hz: Hertz (Grundeinheit)
kHz: Kilohertz (10³ Hz)
MHz: Megahertz (10⁶ Hz)
GHz: Gigahertz (10⁹ Hz)
THz: Terahertz (10¹² Hz)
Zeit-Einheiten:
s: Sekunde (Grundeinheit)
ms: Millisekunde (10⁻³ s)
µs: Mikrosekunde (10⁻⁶ s)
ns: Nanosekunde (10⁻⁹ s)
ps: Pikosekunde (10⁻¹² s)

Design-Hinweise

Praktische Überlegungen
  • Nyquist-Kriterium: Abtastfrequenz mindestens doppelt so hoch wie höchste Signalfrequenz
  • Bandbreite: Frequenzbereich beeinflusst Systemdesign
  • Resonanz: Frequenz bestimmt Resonanzverhalten von Schwingkreisen
  • Phasenbeziehungen: Frequenz beeinflusst Phasenverschiebungen
  • Frequenzstabilität: Präzision abhängig von Referenzoszillatoren
  • EMV: Harmonische der Grundfrequenz beachten

Wechselstrom Funktionen

Kenngrößen der Wechselspannung • Frequenz und Periodendauer • Frequenz und Wellenlänge • Spannungswert zu einem Winkel • Spannungswert an einem Zeitpunkt • Effektivwert einer Sinusschwingung • Effektivwert einer Sinusschwingung mit Offset • Effektivwert eines Sinusimpuls (Einweg) • Effektivwert eines Sinusimpuls (Zweiweg) • Effektivwert einer Rechteckspannung • Effektivwert eines Rechteckimpuls • Effektivwert einer Dreieckspannung • Effektivwert eines Dreieckimpuls • Effektivwert Sägezahnspannung • Effektivwert eines Sägezahnimpuls