Kenngrößen der Wechselspannung

Rechner und Formeln zur Berechnung von Effektiv- und Mittelwert bei Wechselspannung

Sinuskenngrößen berechnen

Wechselspannungs-Parameter

Diese Funktion berechnet aus der angegebenen Spannung die Sinuskenngrößen für die Effektivspannung, Spitzenspannung, Spitze-Spitze-Spannung und Gleichrichtspannung. Für die Eingabe ist die Effektivspannung voreingestellt.

V
Ergebnisse
Effektivspannung:
Spitzenspannung:
Spitze-Spitze-Spannung:
Gleichrichtspannung:

Sinuskenngrößen

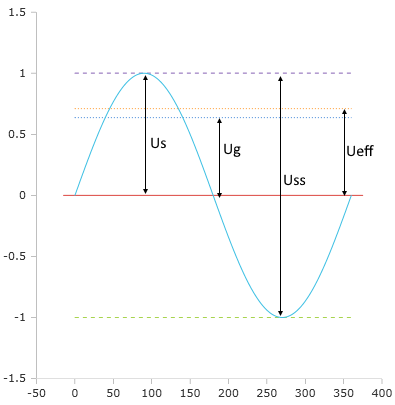
Kenngrößen der Sinusspannung

Kenngrößen der Sinusspannung

Parameter
\(\displaystyle U_{eff}\) = Effektivspannung [V]
\(\displaystyle U_s\) = Spitzenspannung [V]
\(\displaystyle U_{ss}\) = Spitze-Spitze-Spannung [V]
\(\displaystyle U_g\) = Gleichrichtspannung [V]
Grundformeln
\[U_{eff} = \frac{U_s}{\sqrt{2}}\]
\[U_s = U_{eff} \cdot \sqrt{2}\]
\[U_{ss} = 2 \cdot U_s\]

Umrechnungsfaktoren

Faktoren zwischen den Kenngrößen

Von Effektivwert zu:
Spitzenspannung:
× √2 ≈ × 1,414
Spitze-Spitze:
× 2√2 ≈ × 2,828
Gleichrichtwert:
÷ 1,11 ≈ × 0,9
Zu Effektivwert von:
Spitzenspannung:
÷ √2 ≈ × 0,707
Spitze-Spitze:
÷ 2√2 ≈ × 0,354
Gleichrichtwert:
× 1,11

Beispielrechnungen

Praktische Rechenbeispiele

Beispiel 1: Netzspannung (230V Effektivwert)

Gegeben: Ueff = 230V (europäische Netzspannung)

\[U_s = 230V \times \sqrt{2} = 325{,}3V\]
\[U_{ss} = 2 \times 325{,}3V = 650{,}5V\]
\[U_g = \frac{230V}{1{,}11} = 207{,}2V\]
Haushaltsübliche Wechselspannung
Beispiel 2: Niederspannung (12V Effektivwert)

Gegeben: Ueff = 12V (Kleinspannung)

\[U_s = 12V \times \sqrt{2} = 17{,}0V\]
\[U_{ss} = 2 \times 17{,}0V = 33{,}9V\]
\[U_g = \frac{12V}{1{,}11} = 10{,}8V\]
Typische Niederspannungsanwendung
Beispiel 3: Signalspannung (1V Spitze)

Gegeben: Us = 1V (Spitzenspannung)

\[U_{eff} = \frac{1V}{\sqrt{2}} = 0{,}707V\]
\[U_{ss} = 2 \times 1V = 2{,}0V\]
\[U_g = \frac{0{,}707V}{1{,}11} = 0{,}637V\]
Typische Signalverarbeitungsebene
Verhältnisse der Kenngrößen
Scheitelfaktor:
Us / Ueff: √2 ≈ 1,414
Crest Factor
Formfaktor:
Ueff / Ug: 1,11
Form Factor
Spitze-Spitze:
Uss / Us: 2
Peak-to-Peak
Gleichrichtwert:
Ug / Us: 2/π ≈ 0,637
Average Value

Kenngrößen und Formeln

Wechselspannungserzeugung

Bei der Spannungserzeugung in einem rotierenden Generator wird eine zeitlich sinusförmig verlaufende und sich gleichzeitig periodisch wiederholende Wechselspannung erzeugt.

Nennwert und Effektivwert

Der Effektivwert einer Wechselspannung Ueff ist der Wert, der in einem Widerstand die gleiche Wärme erzeugt, wie eine gleich große Gleichspannung. Bei der Nennung „230 V" für die haushaltsübliche Wechselspannung handelt es sich um den Effektivwert.

Wenn der Spitzenwert bekannt ist, kann der Effektivwert nach der folgenden Formel berechnet werden:

Effektivwert-Formel
\[U_{eff} = \frac{U_s}{\sqrt{2}}\]

Der Effektivwert entspricht dem RMS-Wert (Root Mean Square).

Maximalwert, Spitzenwert, Scheitelwert, Amplitude

Der Spitzenwert ist bei sinusförmigem Verlauf die höchste erreichbare Spannungshöhe. Man kann bei gegebenem Effektivwert den Spitzenwert nach folgender Formel berechnen:

Spitzenwert-Formel
\[U_s = U_{eff} \cdot \sqrt{2}\]

Der Spitzenwert ist √2-mal größer als der Effektivwert.

Schwingungsbreite, Spitze-Spitze-Spannung

Die Spitze-Spitze-Spannung Uss ist die Differenz zwischen dem positiven und negativen Spitzenwert und damit das Doppelte des Spitzenwerts.

Spitze-Spitze-Formel
\[U_{ss} = 2 \cdot U_s\]

Die Spitze-Spitze-Spannung umfasst den gesamten Spannungsbereich.

Gleichrichtwert

Der Gleichrichtwert ist der arithmetische Mittelwert der gleichgerichteten Wechselspannung. Bei reinen Sinusspannungen kann er einfach errechnet werden, indem man die Effektivspannung durch 1,111 teilt.

Gleichrichtwert-Formel
\[U_g = \frac{U_{eff}}{1{,}11}\]

Der Gleichrichtwert entspricht dem arithmetischen Mittelwert nach Vollweggleichrichtung.

Wichtige Faktoren

Formfaktor

Der Formfaktor gibt das Verhältnis des Effektivwertes zum Gleichrichtwert an. Bei sinusförmiger Wechselspannung beträgt er 1,111 (exakt π/√8).

\[F = \frac{U_{eff}}{U_g} = 1{,}111\]
Scheitelfaktor

Der Scheitelfaktor ist das Verhältnis des Spitzenwertes zum Effektivwert. Bei einer Sinusspannung liegt der Scheitelfaktor bei 1,414 (exakt √2).

\[C = \frac{U_s}{U_{eff}} = \sqrt{2}\]

Praktische Anwendungen

Elektrotechnik
  • Netzspannungsangaben
  • Transformatorauslegung
  • Isolationskoordination
  • Leistungsberechnungen
Messtechnik
  • Oszilloskop-Messungen
  • Multimeter-Anzeigen
  • Signalanalyse
  • Kalibrierung
Elektronik
  • Verstärkeraussteuerung
  • ADC-Bereichseinstellung
  • Spannungsregler-Design
  • EMV-Betrachtungen

Design-Hinweise

Praktische Überlegungen
  • Spannungsfestigkeit: Bauteile müssen für Spitzenspannung ausgelegt sein
  • Leistungsberechnung: Effektivwerte für thermische Berechnungen verwenden
  • Messgeräte: True-RMS vs. Average-detecting Multimeter unterscheiden
  • Sicherheit: Spitzenspannungen bei Isolationsabständen berücksichtigen
  • Transformatoren: Kernauslegung basiert auf Effektivwerten
  • Kondensatoren: Spannungsfestigkeit mindestens für Spitzenspannung

Wechselstrom Funktionen

Kenngrößen der Wechselspannung • Frequenz und Periodendauer • Frequenz und Wellenlänge • Spannungswert zu einem Winkel • Spannungswert an einem Zeitpunkt • Effektivwert einer Sinusschwingung • Effektivwert einer Sinusschwingung mit Offset • Effektivwert eines Sinusimpuls (Einweg) • Effektivwert eines Sinusimpuls (Zweiweg) • Effektivwert einer Rechteckspannung • Effektivwert eines Rechteckimpuls • Effektivwert einer Dreieckspannung • Effektivwert eines Dreieckimpuls • Effektivwert Sägezahnspannung • Effektivwert eines Sägezahnimpuls