Effektivwert einer Rechteckspannung
Rechner und Formeln zur Berechnung vom Effektivwert einer Rechteckspannung
Rechteckspannung Rechner
Rechteckspannung (50% Tastverhältnis)
Es wird davon ausgegangen, dass die Impulsdauer (ti) und die Pause (tp) die gleiche Länge haben (50% Tastverhältnis).
Rechteckspannung & Parameter
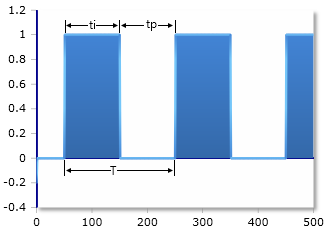
Parameter
Formeln (50% Tastverhältnis)
Beispielrechnungen
Praktische Rechenbeispiele
Beispiel 1: Standard Rechteckspannung
Gegeben: Us = 10V (50% Tastverhältnis)
Beispiel 2: Digitale Logikspannung
Gegeben: Us = 5V (TTL-Pegel, 50% duty cycle)
Beispiel 3: Symmetrische Wechselspannung
Gegeben: Us = 10V (±5V Rechteck-Wechselspannung)
Vergleich der Rechteckspannungsarten
Rechteck-Impulsspannung (0V bis Us):
Rechteck-Wechselspannung (-Us bis +Us):
Formeln zur Rechteckspannung
Was ist eine Rechteckspannung?
Der Effektivwert einer Rechteckimpulsspannung hängt von der Art und Weise ab, wie die Spannung sich mit der Zeit verändert. Eine Rechteckimpulsspannung hat in der Regel einen festen Spitzenwert Us und variiert zwischen zwei Spannungswerten über die Zeit, zum Beispiel Us und 0 V oder Us und -Us.
Der Rechner oben berechnet die Variante mit Us und 0 V. Die Zeit von Us und 0 V (ti und tp) ist je 50%. Einen Rechner für die Variante mit variabler Impulslänge finden Sie hier.
Definition des Effektivwerts
Der Effektivwert ist definiert als Gleichstromwert mit der gleichen Wärmewirkung wie der betrachtete Wechselstrom.
Rechteck-Impulsspannung (0V bis Us)

Der Effektivwert beträgt bei Rechteckspannungen deren Impulsdauer (ti) und Pause (tp) die gleiche Länge haben:
Effektivwert
Etwa 70,7% der Spitzenspannung.
Mittelwert
Die halbe Spitzenspannung.
Rechteck-Wechselspannung (-Us bis +Us)
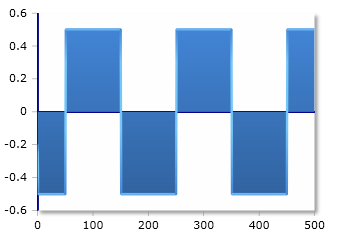
Bei einer symmetrischen Rechteck-Wechselspannung ist der Effektivwert gleich dem Spitzenwert:
Symmetrische Wechselspannung
Da die Spannung in beiden Fällen denselben Betrag (aber mit unterschiedlichem Vorzeichen) hat, bleibt der Effektivwert gleich dem Amplitudenwert der Rechteckspannung.
Der Mittelwert ist bei einer symmetrischen Rechteck-Wechselspannung immer 0 Volt.
Mathematische Herleitung
Berechnung des Effektivwerts
Für eine Rechteckspannung mit 50% Tastverhältnis über eine Periode T:
Praktische Anwendungen
Digitaltechnik
- TTL/CMOS Logikpegel
- Taktsignale (50% duty cycle)
- Datenübertragung
- Mikrocontroller-Ausgänge
Leistungselektronik
- Wechselrichter
- DC-AC Wandler
- H-Brücken
- Motoransteuerung
Signalverarbeitung
- Modulationsverfahren
- Referenzsignale
- Testsignale
- Kalibrierung
Spektrale Eigenschaften
Harmonische bei Rechteckspannungen
Rechteckspannungen enthalten alle ungeraden Harmonischen:
Design-Hinweise
Praktische Überlegungen
- Verlustleistung: P = Ueff²/R - bei 50% duty cycle reduziert
- EMV: Rechteckspannungen erzeugen viele Harmonische
- Filterung: Tiefpässe zur Harmonischen-Unterdrückung notwendig
- Schaltzeiten: Reale Rechteckspannungen haben endliche Flankenzeiten
- Kopplung: Transformatoren für AC-Übertragung geeignet
- Messtechnik: True-RMS Messgeräte für korrekte Effektivwert-Messung
|
|