Elektrische Spannung zu einem Zeitpunkt

Berechnet eine Wechselspannung zu einem bestimmten Zeitpunkt

Spannung zum Zeitpunkt berechnen

Momentanwert-Rechner

Auf dieser Seite können Sie den Momentanwert einer Sinusschwingung zu einem bestimmten Zeitpunkt berechnen. Die Spannung kann als Effektivwert oder als Spitzenspannung eingegeben werden.

V
Ergebnisse
Effektivspannung:
Spitzenspannung:
Momentanspannung:

Sinuswellen-Momentanwerte

Sinuswellen-Momentanwerte

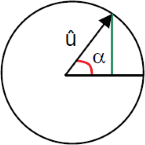
Momentanwerte einer Sinuswelle zu verschiedenen Zeitpunkten

Charakteristische Werte
α = 0° u = 0V
α = 90° u = û (Maximum)
α = 180° u = 0V
α = 270° u = -û (Minimum)
α = 360° u = 0V
Parameter
\(\displaystyle û\) = Spitzenspannung [V]
\(\displaystyle u\) = Momentanspannung [V]
\(\displaystyle f\) = Frequenz [Hz]
\(\displaystyle t\) = Zeitpunkt [s]
\(\displaystyle \omega\) = Kreisfrequenz [rad/s]

Formeln zur Berechnung des Momentanwerts

Grundformeln für Sinuswellen

Kreisfrequenz
\[\omega = 2\pi f\]

Die Kreisfrequenz verknüpft Frequenz mit dem Winkel.

Momentanspannung
\[u(t) = û \cdot \sin(\omega t)\]

Spannung zu einem bestimmten Zeitpunkt t.

Vollständige Formel
\[u(t) = û \cdot \sin(2\pi f \cdot t)\]

Direkter Zusammenhang zwischen Frequenz, Zeit und Momentanspannung.

Wichtiger Hinweis

Radiant-Modus: Zur Berechnung der Formeln muss der Taschenrechner auf Radiant eingestellt sein. Für Berechnungen in Grad verwenden Sie: \(u = û \cdot \sin\left(2\pi f \cdot t \cdot \frac{180}{\pi}\right)\)

Beispielrechnungen

Praktische Rechenbeispiele

Beispiel 1: Netzspannung nach 5ms

Gegeben: Ueff = 230V, f = 50Hz, t = 5ms

\[û = 230V \times \sqrt{2} = 325{,}3V\]
\[\omega = 2\pi \times 50Hz = 314{,}16 \text{ rad/s}\]
\[u(5ms) = 325{,}3V \times \sin(314{,}16 \times 0{,}005) = 325{,}3V \times \sin(1{,}571) = 325{,}3V\]
Momentanspannung entspricht der Spitzenspannung (90°-Position)
Beispiel 2: Audiosignal bei 1kHz

Gegeben: û = 1V, f = 1kHz, t = 0,25ms

\[\omega = 2\pi \times 1000Hz = 6283{,}2 \text{ rad/s}\]
\[u(0{,}25ms) = 1V \times \sin(6283{,}2 \times 0{,}00025) = 1V \times \sin(1{,}571) = 1V\]
90°-Position in der Audioschwingung
Beispiel 3: Hochfrequenzsignal

Gegeben: û = 5V, f = 1MHz, t = 125ns

\[\omega = 2\pi \times 10^6Hz = 6{,}283 \times 10^6 \text{ rad/s}\]
\[u(125ns) = 5V \times \sin(6{,}283 \times 10^6 \times 125 \times 10^{-9}) = 5V \times \sin(0{,}785) = 3{,}54V\]
45°-Position bei Hochfrequenz
Wichtige Zeitpunkte in der Sinuswelle
Nulldurchgänge:
t = 0: u = 0V
t = T/2: u = 0V
t = T: u = 0V
Maxima:
t = T/4: u = +û
t = 3T/4: u = -û
ωt = π/2: Maximum
Steigungen:
t = 0: max. Steigung
t = T/4: Steigung = 0
t = T/2: max. Steigung
Phase:
0°: ωt = 0
90°: ωt = π/2
180°: ωt = π

Theorie der Momentanwerte

Grundlagen der Momentanwertberechnung

Der Spannungswert zu einem bestimmten Zeitpunkt kann auf verschiedene Weisen berechnet oder gemessen werden, abhängig von der Art des Systems. In der Regel bezieht sich dies auf die elektrische Spannung in einem Schaltkreis oder einer Schaltung zu einem gegebenen Moment. Um den Spannungswert zu einem bestimmten Zeitpunkt zu ermitteln, muss man die mathematische Beschreibung der Spannung kennen.

Sinusförmige Wechselspannungen

Falls es sich um eine sinusförmige Wechselspannung handelt, kann die folgende Gleichung verwendet werden. Mit Hilfe der Kreisfrequenzformeln lässt sich der Momentanwert von Spannung und Strom nach einer bestimmten Zeit t bestimmen.

Für Spannungen
\[u(t) = û \cdot \sin(\omega t)\]
\[u(t) = û \cdot \sin(2\pi f t)\]
Für Ströme
\[i(t) = î \cdot \sin(\omega t)\]
\[i(t) = î \cdot \sin(2\pi f t)\]

Umrechnung zwischen Grad und Radiant

Wenn Sie in Grad rechnen möchten, müssen Sie den Parameter für sin in Grad umwandeln:

Umrechnung in Grad
\[u = û \cdot \sin\left(2\pi f \cdot t \cdot \frac{180}{\pi}\right)\]

Multiplizieren Sie das Argument mit 180/π für Gradberechnung.

Praktische Anwendungen

Messtechnik
  • Oszilloskop-Messungen
  • Abtastwert-Bestimmung
  • Signalanalyse
  • Phasenmessungen
Elektronik
  • ADC-Sampling
  • PWM-Erzeugung
  • Synchronisation
  • Triggering
Simulation
  • SPICE-Modelle
  • Zeitbereichsanalyse
  • Transientenrechnung
  • Signalgenerierung

Design-Hinweise

Praktische Überlegungen
  • Abtasttheorem: Abtastrate mindestens 2× höher als höchste Signalfrequenz
  • Phasenbeziehungen: Zeitverschiebungen beeinflussen Momentanwerte
  • Harmonische: Reale Signale enthalten oft Oberwellen
  • Rauschen: Störungen überlagern sich dem Nutzsignal
  • Drift: Frequenz- und Amplitudenstabilität beachten
  • Trigger: Genaue Zeitreferenzen für Messungen erforderlich

Wechselstrom Funktionen

Kenngrößen der Wechselspannung • Frequenz und Periodendauer • Frequenz und Wellenlänge • Spannungswert zu einem Winkel • Spannungswert an einem Zeitpunkt • Effektivwert einer Sinusschwingung • Effektivwert einer Sinusschwingung mit Offset • Effektivwert eines Sinusimpuls (Einweg) • Effektivwert eines Sinusimpuls (Zweiweg) • Effektivwert einer Rechteckspannung • Effektivwert eines Rechteckimpuls • Effektivwert einer Dreieckspannung • Effektivwert eines Dreieckimpuls • Effektivwert Sägezahnspannung • Effektivwert eines Sägezahnimpuls