Effektivwert eines Sägezahnimpuls

Rechner und Formeln zur Berechnung des Effektivwert einer Sägezahnimpuls-Spannung

Sägezahnimpuls Rechner

Sägezahnimpuls-Spannung

Geben Sie die Werte der Impulsdauer (ti), der Periodendauer (T) und die Spitzenspannung Us des Impulses ein.

ms
ms
V
Ergebnisse
Effektivspannung:
Mittelspannung:

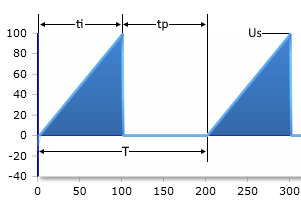
Sägezahnimpuls & Parameter

Sägezahnimpuls
Parameter
\(\displaystyle U_s\) = Spitzenspannung [V]
\(\displaystyle U_{eff}\) = Effektivspannung [V]
\(\displaystyle U_m\) = Mittelspannung [V]
\(\displaystyle T\) = Periodendauer [ms]
\(\displaystyle t_i\) = Impulsdauer [ms]
Grundformeln
\[U_{eff} = \sqrt{\frac{t_i}{T \cdot 3}} \cdot U_s\]
\[U_m = \frac{U_s \cdot t_i}{2 \cdot T}\]

Beispielrechnungen

Praktische Rechenbeispiele

Beispiel 1: 50% Tastverhältnis

Gegeben: Us = 10V, ti = 50ms, T = 100ms

\[U_{eff} = \sqrt{\frac{50}{100 \cdot 3}} \cdot 10V = \sqrt{\frac{1}{6}} \cdot 10V = 4{,}08V\]
\[U_m = \frac{10V \cdot 50ms}{2 \cdot 100ms} = \frac{500}{200} = 2{,}5V\]
Typisches Sägezahnsignal mit 50% duty cycle
Beispiel 2: 25% Tastverhältnis

Gegeben: Us = 12V, ti = 25ms, T = 100ms

\[U_{eff} = \sqrt{\frac{25}{100 \cdot 3}} \cdot 12V = \sqrt{\frac{1}{12}} \cdot 12V = 3{,}46V\]
\[U_m = \frac{12V \cdot 25ms}{2 \cdot 100ms} = \frac{300}{200} = 1{,}5V\]
Niedriges Tastverhältnis für Energieeinsparung
Beispiel 3: Oszilloskop-Anwendung

Gegeben: Us = 5V, ti = 2ms, T = 10ms (20% duty cycle)

\[U_{eff} = \sqrt{\frac{2}{10 \cdot 3}} \cdot 5V = \sqrt{\frac{1}{15}} \cdot 5V = 1{,}29V\]
\[U_m = \frac{5V \cdot 2ms}{2 \cdot 10ms} = \frac{10}{20} = 0{,}5V\]
Typisch für Zeitbasis-Generatoren
Tastverhältnis-Auswirkungen bei Sägezahn
Effektivwert-Faktor:
Formel: √(ti/(T·3))
Bei 50%: √(1/6) ≈ 0,408
Bei 25%: √(1/12) ≈ 0,289
Bei 10%: √(1/30) ≈ 0,183
Mittelwert-Faktor:
Formel: ti/(2·T)
Bei 50%: 0,25
Bei 25%: 0,125
Bei 10%: 0,05

Formeln zum Sägezahnimpuls

Was ist ein Sägezahnimpuls?

Der Effektivwert (auch RMS-Wert, Root Mean Square) eines Sägezahnimpulses kann durch die allgemeine Formel für den Effektivwert eines periodischen Signals berechnet werden. Er ist definiert als Gleichstromwert mit der gleichen Wärmewirkung wie der betrachtete Wechselstrom. Er berechnet sich bei Sägezahn-Impulsspannungen nach der folgenden Formel.

Definition des Effektivwerts

Bei einem Sägezahnimpuls steigt die Spannung linear von 0V auf den Spitzenwert Us über die Impulsdauer ti an, und bleibt dann für die restliche Periodendauer bei 0V. Die eingegebenen Parameter für T und ti müssen die gleiche Maßeinheit haben.

Effektivwert
\[U_{eff} = \sqrt{\frac{t_i}{T \cdot 3}} \cdot U_s\]

Abhängig vom Tastverhältnis und Faktor 1/√3.

Mittelwert
\[U_m = \frac{U_s \cdot t_i}{2 \cdot T}\]

Halber Wert des Rechteckimpulses.

Mathematische Herleitung

Berechnung

Für einen Sägezahnimpuls über eine Periode T:

\[U_{eff} = \sqrt{\frac{1}{T} \int_0^T u^2(t) \, dt}\]
Für 0 ≤ t ≤ ti: u(t) = Us · t/ti (linear ansteigend)
Für ti < t ≤ T: u(t) = 0
\[U_{eff} = \sqrt{\frac{1}{T} \int_0^{t_i} \left(\frac{U_s \cdot t}{t_i}\right)^2 dt} = U_s \sqrt{\frac{t_i}{3T}}\]

Praktische Anwendungen

Messtechnik
  • Oszilloskop-Zeitbasis
  • Sweep-Generatoren
  • Spannungsrampen
  • ADC-Testmuster
Signalverarbeitung
  • Frequenz-Modulation
  • VCO-Ansteuerung
  • Wobbler-Signale
  • Linearisierung
Regelungstechnik
  • Rampen-Generator
  • Sollwert-Vorgabe
  • Integrator-Test
  • Zeitsteuerung

Vergleich mit anderen Signalformen

Effektivwert-Faktoren bei 50% Tastverhältnis
Rechteckimpuls:
Ueff = Us/√2 ≈ 0,707
Dreieckimpuls:
Ueff = Us/√3 ≈ 0,577
Sägezahnimpuls:
Ueff = Us/√6 ≈ 0,408
Sinusimpuls:
Ueff = Us/2 = 0,5

Spektrale Eigenschaften

Harmonische bei Sägezahnimpulsen

Sägezahnimpulse enthalten alle Harmonischen mit spezifischer Verteilung:

DC-Anteil: Us · D/2 (D = Tastverhältnis)
Grundwelle: Amplitude proportional zu sin(πD)/(πD)
Harmonische: Amplitude ∝ sin(nπD)/(nπD)²
Besonderheit: Harmonische fallen mit 1/n² ab (schneller als Rechteck)

Design-Hinweise

Praktische Überlegungen
  • Linearität: Konstante Anstiegsgeschwindigkeit wichtig für Präzision
  • Bandbreite: Schnelle Anstiegsflanke erfordert hohe Bandbreite
  • Offsetfehler: Können die Linearität beeinträchtigen
  • Temperaturstabilität: Wichtig für präzise Rampen-Generatoren
  • Rückstellung: Schnelle Rücksetzung auf 0V erforderlich
  • Belastung: Kapazitive Lasten können Linearität verschlechtern

Wechselstrom Funktionen

Kenngrößen der Wechselspannung • Frequenz und Periodendauer • Frequenz und Wellenlänge • Spannungswert zu einem Winkel • Spannungswert an einem Zeitpunkt • Effektivwert einer Sinusschwingung • Effektivwert einer Sinusschwingung mit Offset • Effektivwert eines Sinusimpuls (Einweg) • Effektivwert eines Sinusimpuls (Zweiweg) • Effektivwert einer Rechteckspannung • Effektivwert eines Rechteckimpuls • Effektivwert einer Dreieckspannung • Effektivwert eines Dreieckimpuls • Effektivwert Sägezahnspannung • Effektivwert eines Sägezahnimpuls