Calculate Axial Symmetric Pentagon

Calculator and formulas for the symmetric irregular pentagon

Axial Symmetric Pentagon Calculator

The axial symmetric pentagon

An axial symmetric pentagon is an irregular pentagon with one axis of symmetry. Defined by 3 side lengths and 1 angle.

Enter pentagon parameters
Base of the symmetric pentagon
Symmetric side lengths
Upper symmetric sides
Base angle in degrees
Axial symmetric pentagon

Definition: A pentagon with one vertical axis of symmetry

Base: a Symmetric sides: 2×b, 2×c Base angle: α
Pentagon calculation results
Central angle β:
Base angle γ:
Diagonal d:
Height h:
Perimeter P:
Area A:

Pentagon structure

The axial symmetric pentagon has one vertical axis of symmetry.
Defined by base a, sides b, c and base angle α.

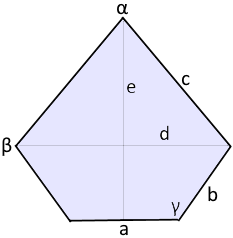
axial symmetric pentagon

The axial symmetric pentagon

An axial symmetric pentagon is a special form of irregular pentagon:

  • One axis of symmetry: Vertical through apex and base center
  • Five sides: Base a, two sides b, two sides c
  • Four parameters: Three lengths and one angle for complete determination
  • Symmetric structure: Reflection along the vertical axis
  • Practical application: Architecture, design, technology
  • Complex calculation: Trigonometric formulas required

Axial symmetry properties

The axial symmetry gives the pentagon special geometric properties:

Axis of symmetry
  • Runs vertically through the pentagon
  • Divides the figure into two congruent halves
  • Intersects base a at its midpoint
  • Passes through the opposite apex
Symmetric elements
  • Two sides of length b (symmetric)
  • Two sides of length c (symmetric)
  • Equal base angles on both sides
  • Symmetric heights and diagonals

Geometric analysis

The geometric properties of the axial symmetric pentagon:

Angle relationships
  • α: Base angle (given)
  • β: Central angle (calculated)
  • γ: Upper base angle (calculated)
  • Sum: 540° (pentagon property)
Distance relationships
  • d: Diagonal (law of cosines)
  • h: Height (Pythagorean application)
  • P: Perimeter = a + 2b + 2c
  • A: Area (complex formula)

Applications of the axial symmetric pentagon

The axial symmetric pentagon finds diverse practical applications:

Architecture & construction
  • House gables and roof forms
  • Window and door openings
  • Decorative facade elements
  • Church windows and rosettes
Mechanical engineering & technology
  • Special tool forms
  • Gear and cam profiles
  • Structural reinforcement ribs
  • Optical components
Design & art
  • Logo design and corporate identity
  • Furniture design and interior architecture
  • Jewelry and decorative objects
  • Textile patterns and ornaments
Nature & biology
  • Leaf forms and botanical structures
  • Crystal growth and minerals
  • Anatomical cross-sections
  • Biomimetic design

Formulas for the axial symmetric pentagon

Diagonal d
\[d = \sqrt{2c^2 - 2c^2\cos(\alpha)}\]

Law of cosines for the main diagonal

Perimeter P
\[P = a + 2b + 2c\]

Sum of all five side lengths

Height h
\[h = \sqrt{b^2 - \left(\frac{d}{2} - \frac{a}{2}\right)^2} + \sqrt{c^2 - \left(\frac{d}{2}\right)^2}\]

Sum of height segments using Pythagorean theorem

Central angle β
\[\beta = \arccos\left(\frac{b^2 + c^2 - e^2 - (\frac{a}{2})^2}{2bc}\right)\]

Law of cosines applied to the central triangle

Base angle γ
\[\gamma = \frac{540° - \alpha - 2\beta}{2}\]

From the pentagon interior angle sum

Area A
\[A = \frac{1}{4}\sqrt{(d+a)^2(d-a+2b)(a-d+2b)} + \frac{1}{2}\sqrt{\frac{4c^2-d^2}{4}} \cdot d\]

Complex area formula from two triangle portions

Calculation example for an axial symmetric pentagon

Given
Base a = 8 Side b = 6 Side c = 5 Angle α = 70°

Find: All geometric properties of the symmetric pentagon

1. Basic calculations
\[d = \sqrt{2 \times 25 - 50\cos(70°)} = 6.40\] \[P = 8 + 2 \times 6 + 2 \times 5 = 30\]

Calculate diagonal and perimeter

2. Angle calculation
\[\beta = \arccos(...) \approx 85.2°\] \[\gamma = \frac{540° - 70° - 2 \times 85.2°}{2} = 147.3°\]

Central and upper base angles

3. Height and area
Height h ≈ 8.45
Area A ≈ 33.8

Complex calculations using Pythagorean theorem and area formulas

4. Complete axial symmetric pentagon
Base a = 8.00 Sides b = 6.00 Sides c = 5.00 Base angle α = 70.0°
Central angle β = 85.2° Upper angle γ = 147.3° Diagonal d = 6.40 Perfect symmetry!

The complete symmetric pentagon - a harmonious geometric form

The axial symmetric pentagon: Geometry of balance

The axial symmetric pentagon is a fascinating example of how symmetry and irregularity can coexist in geometry. As a pentagon with a single axis of reflection, it connects the structural simplicity of regular forms with the flexibility of irregular polygons, finding diverse applications in architecture, design, and technical constructions.

Symmetry as organizing principle

The axial symmetry gives the pentagon special properties:

  • One axis of reflection: Vertical through apex and base midpoint
  • Paired symmetry: Two sides b and two sides c are equal respectively
  • Reduced complexity: Only 4 parameters instead of 8 for general pentagon
  • Unique determination: Three lengths and one angle suffice
  • Calculable properties: All other measures follow from basic parameters
  • Aesthetic balance: Visually appealing, harmonious proportions

Mathematical challenges

Calculating axial symmetric pentagons requires advanced geometry:

Trigonometric methods

Law of cosines and law of sines enable calculation of unknown sides and angles from given parameters.

Complex area calculation

The area requires decomposition into triangles and application of special area formulas.

Height determination

The total height is composed of different height segments calculated using the Pythagorean theorem.

Angle relationships

The interior angle sum of 540° (pentagon property) enables calculation of unknown angles.

Practical applications in the real world

The axial symmetric pentagon finds broad practical application:

  • Architectural gables: House forms with pentagon silhouette
  • Industrial design: Tools and components with optimized functionality
  • Optical systems: Lenses and prisms with special properties
  • Structural mechanics: Reinforcement ribs and support elements
  • Packaging design: Efficient and aesthetic container forms
  • Artistic design: Logos, ornaments and decorative elements

Connection to other geometric concepts

The axial symmetric pentagon connects various geometric principles:

Symmetry theory

As an example of partial symmetry, it shows how a single axis of reflection organizes and simplifies complex forms.

Trigonometry

The application of sine, cosine, and tangent functions to solve complex geometric problems.

Analytic geometry

Coordinate systems and algebraic methods complement classical Euclidean geometry.

Optimization

In technical applications often basis for optimization problems regarding area, perimeter, or material consumption.

Summary

The axial symmetric pentagon stands as elegant proof that symmetry does not mean perfection, but rather balance and order in diversity. Its mathematical treatment connects elementary geometry with advanced trigonometric methods and shows how complex structures can arise from few basic parameters. In a world increasingly seeking functional aesthetics, the axial symmetric pentagon offers a perfect synthesis of mathematical precision and practical applicability. It teaches us that true geometric beauty lies not in absolute regularity, but in intelligent balance between order and variation - a principle confirmed again and again from nature to modern architecture.

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?

More polygons

Triangle • Square • Pentagon • Hexagon • Heptagon • Octagon • Nonagon • Decagon • Hendecagon • Dodecagon • Hexadecagon • N-Gon • Polygon ring • Concave hexagon • Axial Symmetric Pentagon • Irregular, stretched Hexagon • Irregular, stretched Octagon • Pentagram • Hexagram • Octagram • Star of Lakshmi