Hexadecagon (16-gon) Calculator
Calculator and formulas for regular hexadecagons
Hexadecagon Calculator
Regular Hexadecagon
A regular hexadecagon has 16 equal sides and 16 equal interior angles (157.5°). 16 = 2⁴ (power of 2).
Regular Hexadecagon
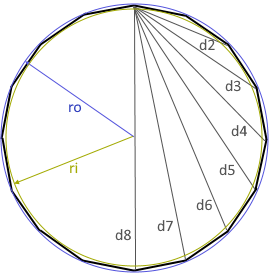
The diagram shows a regular hexadecagon with all relevant parameters.
All 16 sides are equal in length, all interior angles measure 157.5°.
Properties of a regular hexadecagon
A regular hexadecagon (hexadecagon) is a highly symmetric geometric object:
- 16 equal sides: All side lengths are identical
- 16 equal angles: Each interior angle measures exactly 157.5°
- Sum of angles: 14 × 180° = 2520°
- Power of 2: 16 = 2⁴ - special properties
- Central angle: 360°/16 = 22.5° per segment
- Construction: Very easy to construct
The hexadecagon and binary systems
The regular hexadecagon benefits from its power-of-2 property:
Binary properties
- 16 = 2⁴ (4th power of 2)
- Binary: 10000 (5 bits)
- Hexadecimal: 10 (1 hexadecimal digit)
- Easy halving possible
Divisibility properties
- Divisible by: 1, 2, 4, 8, 16
- Symmetric subdivisions possible
- Octagon (8-gon) as half
- Square (4-gon) as quarter
Construction and mathematical elegance
The regular hexadecagon is particularly construction-friendly:
Simple construction
- Very easy with compass and straightedge
- Through repeated angle bisection
- 22.5° = 45°/2 = 90°/4
- Central angle exactly constructible
Trigonometric values
- sin(22.5°) = √(2-√2)/2
- cos(22.5°) = √(2+√2)/2
- Exact algebraic expressions
- Simple calculations possible
Applications of the regular hexadecagon
Regular hexadecagons find wide practical application:
Navigation & orientation
- Precise compass roses (22.5° steps)
- Wind direction indicators
- Nautical navigation aids
- Astronomical instruments
Architecture & design
- Dome constructions
- Window mosaics and rosettes
- Floor coverings and tile patterns
- Decorative architectural elements
Mechanical engineering & technology
- High-precision gears
- Bearing and coupling designs
- Rotationally symmetric components
- Machine tool components
Digital technology & computing
- Encoder discs (4-bit resolution)
- Digital encoders and sensors
- Algorithm design for 2⁴ structures
- Computer graphics and game design
Formulas for the regular hexadecagon
Area A
With cot(π/16) ≈ 5.027
Perimeter P
Simple: 16 times the side length
Diagonal d₂
Shortest diagonal
Diagonal d₄
With √2/2 (45° relation)
Diagonal d₈ (longest)
Diameter of the circumcircle
Other diagonals
Systematic progression
Circumradius rₐ
With sin(π/16) ≈ 0.195
Inradius rᵢ
Apothem of the hexadecagon
Calculation example for a hexadecagon
Given
Find: All properties of the regular hexadecagon
1. Calculate basic measures
Perimeter and area
2. Calculate radii
Circumradius and inradius
3. All diagonals (selection)
All seven different diagonal lengths
4. Complete summary
Complete characterization of the regular hexadecagon
The regular hexadecagon in science and technology
The regular hexadecagon occupies a special position, as it brings ideal properties for technical applications and digital systems as a power of 2 (16 = 2⁴). This mathematical property makes it a preferred element in precision engineering and computer systems.
Power-of-2 properties and their advantages
The properties as the 4th power of 2 give the hexadecagon unique advantages:
- Binary compatibility: 16 = 2⁴ corresponds to 4 bits in digital systems
- Simple divisibility: Evenly divisible by 1, 2, 4, 8, 16
- Constructive simplicity: Central angle 22.5° = 90°/4 exactly constructible
- Symmetry hierarchy: Contains square (4), octagon (8) as subdivisions
- Computer-friendly: Ideal for algorithm-based calculations
Precision engineering and measurement technology
In precision engineering, the hexadecagon offers special advantages:
Encoder technology
16-position encoders offer 4-bit resolution with perfect binary representation. Each position corresponds exactly to a 4-bit code from 0000 to 1111.
Precision mechanics
High-precision gears and couplings use 16-fold symmetry for even force distribution and minimal vibration.
Navigation and orientation
22.5° steps enable precise direction indications. 16 directions cover all main directions (N, NNE, NE, ENE, etc.).
Measurement and calibration systems
Standard reference for turntables, rotary tables and angle measuring devices in quality assurance.
Digital applications and algorithms
The hexadecagon finds wide application in digital systems:
- Computer graphics: 16-fold rotational symmetry for 3D models and animations
- Signal processing: 16-point FFT and digital filter designs
- Game design: Movement directions in games (16-way control)
- User interface: Radial menus with 16 options for touch interfaces
- Robotics: Sensor arrays and omnidirectional movement control
- Image processing: Template matching and object recognition
Modern manufacturing technology
In modern production, the hexadecagon offers practical advantages:
CNC machining
Standard G-code programs for 16-sided machining. Indexable tool changers often use 16-position magazines.
3D printing and rapid prototyping
Optimal balance between precision and printing time. 16 facets provide good circle approximation with reasonable effort.
Quality assurance
Standardized test specimens and reference objects. Coordinate measuring machines use 16-point circle measurements.
Automation
Conveyor systems, sorting machines and pick-and-place robots use 16-fold division for optimal workstations.
Summary
The regular hexadecagon represents the perfect connection between classical geometry and modern technology. Its properties as a power of 2 make it an ideal interface between analog and digital worlds. From precision mechanics through computer graphics to modern manufacturing technologies, the hexadecagon shows how mathematical elegance can solve practical problems. It stands as a symbol of the efficiency that arises when geometry and binary systems harmonize.
|
|