Heptagon (7-gon) Calculator
Calculator and formulas for regular heptagons
Heptagon Calculator
Regular Heptagon
A regular heptagon has 7 equal sides and 7 equal interior angles (≈128.57°). The number 7 is a prime number.
Regular Heptagon
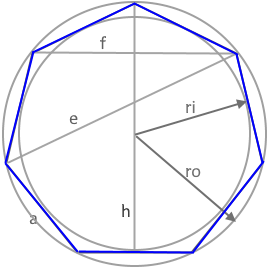
The diagram shows a regular heptagon with all relevant parameters.
All 7 sides are equal in length, all interior angles measure ≈128.57°.
Properties of a regular heptagon
A regular heptagon (septagon) is a fascinating geometric object:
- 7 equal sides: All side lengths are identical
- 7 equal angles: Each interior angle measures ≈128.571°
- Sum of angles: 5 × 180° = 900°
- Prime number 7: Special mathematical properties
- Central angle: 360°/7 ≈ 51.429° per segment
- Construction: Complex geometric challenge
The heptagon and the mystical number 7
The regular heptagon embodies the special properties of the number 7:
Cultural significance
- 7 is a "magical" number in many cultures
- 7 days of the week, 7 wonders of the world, 7 colors of rainbow
- Religious and mythological significance
- Psychological "magic number seven"
Mathematical properties
- 7 is a prime number (indivisible)
- Mersenne prime: 2³-1 = 7
- First safe prime
- 360°/7 is irrational
Construction and geometric challenges
The regular heptagon presents special constructive challenges:
Classical construction
- Constructible with compass and straightedge (Gauss)
- Requires complex algebraic constructions
- Practical approximation methods available
- Central angle: 360°/7 ≈ 51.429°
Trigonometric values
- cos(π/7) and sin(π/7) are algebraic
- Exact values are very complex
- Approximations: sin(π/7) ≈ 0.4339
- cos(π/7) ≈ 0.9010
Applications of the regular heptagon
Regular heptagons find diverse applications:
Coinage & medals
- British 20 and 50 pence coins
- Special coins from various countries
- Collector medals and commemorative coins
- Historical coin shapes
Art & architecture
- Gothic rose windows
- Islamic ornaments and mosaics
- Modern architectural elements
- Decorative art and design
Games & culture
- 7-sided dice (rare)
- Symbolism in literature and film
- Cultural and religious representations
- Logos and corporate design
Science & technology
- Crystallography and molecular structures
- Optical systems and apertures
- Rotationally symmetric components
- Sensor arrays and measurement technology
Formulas for the regular heptagon
Area A
With cot(π/7) ≈ 2.077
Perimeter P
Simple: 7 times the side length
Diagonal e (short)
Shorter of the two diagonal types
Diagonal f (long)
Longer of the two diagonal types
Height h
With tan(π/14) ≈ 0.2218
Circumradius ro
With sin(π/7) ≈ 0.4339
Inradius ri
With tan(π/7) ≈ 0.4816
Interior angle α
Each of the 7 interior angles
Calculation example for a heptagon
Given
Find: All properties of the regular heptagon
1. Calculate basic measures
Perimeter and area
2. Calculate radii and height
Radii and height
3. Calculate diagonals
The two different diagonal types
4. Complete summary
Complete characterization of the regular heptagon
The regular heptagon in culture and science
The regular heptagon occupies a very special position, as the number 7 has mystical and symbolic meaning in almost all cultures of the world. This cultural significance combines with interesting mathematical properties to create a fascinating geometric object.
The mystical number 7 and its geometric manifestation
The number 7 permeates human culture like no other:
- Temporal structures: 7 days of the week have shaped our lives for millennia
- Religious symbolism: 7 days of creation, 7 virtues, 7 deadly sins
- Cultural manifestations: 7 wonders of the world, 7 dwarfs, 7 years of bad luck
- Psychological significance: "Magic Number Seven" in cognitive research
- Mathematical uniqueness: Prime number with special properties
Geometric and mathematical challenges
The regular heptagon presents special mathematical challenges:
Constructive aspects
Construction with compass and straightedge is theoretically possible, but practically very complex. This is due to the trigonometric properties of the number 7.
Numerical properties
The values of sin(π/7) and cos(π/7) are algebraic numbers, but their exact form is very complicated.
Practical applications
Despite constructive difficulties, the heptagon finds practical application, especially in coinage and architecture.
Symmetry properties
The 7-fold rotational symmetry and associated symmetry groups are of theoretical interest.
Practical applications and cultural significance
The heptagon finds diverse practical applications:
- Coinage: British 20p and 50p coins use the heptagonal shape
- Architecture: Gothic rose windows and Islamic ornaments
- Design: Logos and corporate identity use the symbolic power of 7
- Science: Crystal structures and molecular arrangements
- Games: Rare 7-sided dice and game elements
Modern computational aspects
In the digital world, the heptagon gains new meaning:
Algorithmic Design
CAD systems and computer graphics use efficient algorithms for generating and calculating heptagons.
Signal Processing
The 7-fold symmetry finds application in digital signal processing and image analysis.
Crystallography
Quasicrystals and theoretical 7-fold symmetric structures are subjects of current research.
User Interface Design
The psychological significance of 7 is used in designing user interfaces and menu systems.
Summary
The regular heptagon stands as a unique example of the connection between mathematics, culture, and practical application. The mystical meaning of the number 7 gives this geometric object a cultural dimension that goes far beyond its purely mathematical properties. From ancient religious symbols to modern coins and digital designs, the heptagon shows the timeless fascination that comes from the connection between numbers, shapes, and human culture.
|
|