Siebeneck (Heptagon) berechnen
Rechner und Formeln für regelmäßige Siebenecke
Heptagon Rechner
Regelmäßiges Siebeneck
Ein regelmäßiges Heptagon hat 7 gleich lange Seiten und 7 gleich große Winkel (≈128,57°). Die Zahl 7 ist eine Primzahl.
Regelmäßiges Heptagon
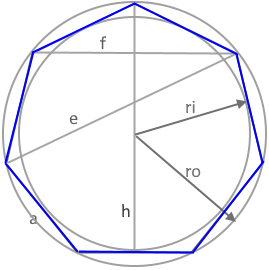
Das Diagramm zeigt ein regelmäßiges Siebeneck mit allen relevanten Parametern.
Alle 7 Seiten sind gleich lang, alle Innenwinkel betragen ≈128,57°.
Eigenschaften eines regelmäßigen Siebenecks
Ein regelmäßiges Siebeneck (Heptagon) ist ein faszinierendes geometrisches Objekt:
- 7 gleiche Seiten: Alle Seitenlängen sind identisch
- 7 gleiche Winkel: Jeder Innenwinkel beträgt ≈128,571°
- Winkelsumme: 5 × 180° = 900°
- Primzahl 7: Besondere mathematische Eigenschaften
- Zentrumswinkel: 360°/7 ≈ 51,429° pro Segment
- Konstruktion: Komplexe geometrische Herausforderung
Das Siebeneck und die mystische Zahl 7
Das regelmäßige Siebeneck verkörpert die besonderen Eigenschaften der Zahl 7:
Kulturelle Bedeutung
- 7 ist eine "magische" Zahl in vielen Kulturen
- 7 Wochentage, 7 Weltwunder, 7 Farben des Regenbogens
- Religiöse und mythologische Bedeutung
- Psychologische "magic number seven"
Mathematische Eigenschaften
- 7 ist eine Primzahl (unteilbar)
- Mersenne-Primzahl: 2³-1 = 7
- Erste sichere Primzahl
- 360°/7 ist irrational
Konstruktion und geometrische Herausforderungen
Das regelmäßige Siebeneck stellt besondere konstruktive Herausforderungen:
Klassische Konstruktion
- Mit Zirkel und Lineal konstruierbar (Gauß)
- Erfordert komplexe algebraische Konstruktionen
- Praktische Näherungsverfahren verfügbar
- Zentrumswinkel: 360°/7 ≈ 51,429°
Trigonometrische Werte
- cos(π/7) und sin(π/7) sind algebraisch
- Exakte Werte sind sehr komplex
- Näherungen: sin(π/7) ≈ 0.4339
- cos(π/7) ≈ 0.9010
Anwendungen des regelmäßigen Siebenecks
Regelmäßige Siebenecke finden vielfältige Anwendungen:
Münzwesen & Medaillen
- Britische 20- und 50-Pence-Münzen
- Sondermünzen verschiedener Länder
- Sammlermedaillen und Gedenkmünzen
- Historische Münzformen
Kunst & Architektur
- Gotische Rosettenfenster
- Islamische Ornamente und Mosaike
- Moderne architektonische Elemente
- Dekorative Kunst und Design
Spiele & Kultur
- Spielwürfel mit 7 Seiten (selten)
- Symbolik in Literatur und Film
- Kulturelle und religiöse Darstellungen
- Logos und Corporate Design
Wissenschaft & Technik
- Kristallographie und Molekularstrukturen
- Optische Systeme und Blenden
- Rotationssymmetrische Bauteile
- Sensor-Arrays und Messtechnik
Formeln für das regelmäßige Siebeneck (Heptagon)
Flächeninhalt A
Mit cot(π/7) ≈ 2.077
Umfang P
Einfach: 7-mal die Seitenlänge
Diagonale e (kurz)
Kürzere der beiden Diagonalarten
Diagonale f (lang)
Längere der beiden Diagonalarten
Höhe h
Mit tan(π/14) ≈ 0.2218
Umkreisradius rₐ
Mit sin(π/7) ≈ 0.4339
Innenkreisradius rᵢ
Mit tan(π/7) ≈ 0.4816
Innenwinkel α
Jeder der 7 Innenwinkel
Rechenbeispiel für ein Heptagon
Gegeben
Gesucht: Alle Eigenschaften des regelmäßigen Siebenecks
1. Grundmaße berechnen
Umfang und Flächeninhalt
2. Radien und Höhe
Radien und Höhe
3. Diagonalen berechnen
Die beiden verschiedenen Diagonalarten
4. Vollständige Zusammenfassung
Komplette Charakterisierung des regelmäßigen Siebenecks
Das regelmäßige Siebeneck in Kultur und Wissenschaft
Das regelmäßige Siebeneck nimmt eine ganz besondere Stellung ein, da die Zahl 7 in nahezu allen Kulturen der Welt eine mystische und symbolische Bedeutung hat. Diese kulturelle Bedeutung verbindet sich mit interessanten mathematischen Eigenschaften zu einem faszinierenden geometrischen Objekt.
Die mystische Zahl 7 und ihre geometrische Manifestation
Die Zahl 7 durchzieht die menschliche Kultur wie keine andere:
- Zeitliche Strukturen: 7 Wochentage prägen unser Leben seit Jahrtausenden
- Religiöse Symbolik: 7 Schöpfungstage, 7 Tugenden, 7 Todsünden
- Kulturelle Manifestationen: 7 Weltwunder, 7 Zwerge, 7 Jahre Unglück
- Psychologische Bedeutung: "Magic Number Seven" in der Kognitionsforschung
- Mathematische Einzigartigkeit: Primzahl mit besonderen Eigenschaften
Geometrische und mathematische Herausforderungen
Das regelmäßige Siebeneck stellt besondere mathematische Herausforderungen dar:
Konstruktive Aspekte
Die Konstruktion mit Zirkel und Lineal ist zwar theoretisch möglich, aber praktisch sehr komplex. Dies liegt an den trigonometrischen Eigenschaften der Zahl 7.
Numerische Eigenschaften
Die Werte von sin(π/7) und cos(π/7) sind algebraische Zahlen, deren exakte Form jedoch sehr kompliziert ist.
Praktische Anwendungen
Trotz der konstruktiven Schwierigkeiten findet das Siebeneck praktische Anwendung, besonders im Münzwesen und in der Architektur.
Symmetrie-Eigenschaften
Die 7-fache Rotationssymmetrie und die damit verbundenen Symmetriegruppen sind von theoretischem Interesse.
Praktische Anwendungen und kulturelle Bedeutung
Das Siebeneck findet vielfältige praktische Anwendungen:
- Münzprägung: Britische 20p und 50p Münzen verwenden die Siebeneck-Form
- Architektur: Gotische Rosettenfenster und islamische Ornamente
- Design: Logos und corporate identity nutzen die symbolische Kraft der 7
- Wissenschaft: Kristallstrukturen und molekulare Arrangements
- Spiele: Seltene 7-seitige Würfel und Spielelemente
Moderne computationale Aspekte
In der digitalen Welt erlangt das Siebeneck neue Bedeutung:
Algorithmic Design
CAD-Systeme und Computergrafik nutzen effiziente Algorithmen zur Generierung und Berechnung von Siebenecken.
Signal Processing
Die 7-fache Symmetrie findet Anwendung in der digitalen Signalverarbeitung und Bildanalyse.
Crystallography
Quasikristalle und theoretische 7-fach symmetrische Strukturen sind Gegenstand aktueller Forschung.
User Interface Design
Die psychologische Bedeutung der 7 wird in der Gestaltung von Benutzeroberflächen und Menüsystemen genutzt.
Zusammenfassung
Das regelmäßige Siebeneck steht als einzigartiges Beispiel für die Verbindung von Mathematik, Kultur und praktischer Anwendung. Die mystische Bedeutung der Zahl 7 verleiht diesem geometrischen Objekt eine kulturelle Dimension, die weit über seine rein mathematischen Eigenschaften hinausgeht. Von antiken religiösen Symbolen bis zu modernen Münzen und digitalen Designs zeigt das Heptagon die zeitlose Faszination, die von der Verbindung zwischen Zahlen, Formen und menschlicher Kultur ausgeht.
|
|