Sechseck (Hexagon) berechnen
Rechner und Formeln für regelmäßige Sechsecke
Hexagon Rechner
Regelmäßiges Sechseck
Ein regelmäßiges Hexagon hat 6 gleich lange Seiten und 6 gleich große Winkel (120°). Es ist die perfekte Form der Natur.
Regelmäßiges Hexagon
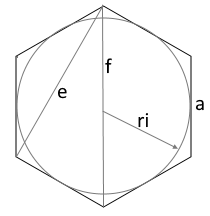
Das Diagramm zeigt ein regelmäßiges Sechseck mit allen relevanten Parametern.
Alle 6 Seiten sind gleich lang, alle Innenwinkel betragen 120°.
Eigenschaften eines regelmäßigen Sechsecks
Ein regelmäßiges Sechseck (Hexagon) ist eine der elegantesten geometrischen Formen:
- 6 gleiche Seiten: Alle Seitenlängen sind identisch
- 6 gleiche Winkel: Jeder Innenwinkel beträgt exakt 120°
- Winkelsumme: 4 × 180° = 720°
- Natürliche Perfektion: Häufigste Form in der Natur
- Zentrumswinkel: 360°/6 = 60° pro Segment
- Tesselation: Perfekte Parkettierung möglich
Das Sechseck in der Natur
Das regelmäßige Sechseck ist die bevorzugte Form der Natur:
Kristallstrukturen
- Schneeflocken zeigen 6-fache Symmetrie
- Quarz und andere Mineralien
- Eis-Kristallgitter (hexagonal)
- Graphit-Schichtstruktur
Biologische Formen
- Bienenwaben (perfekte Raumnutzung)
- Basaltsäulen (Kühlung von Lava)
- Verbindungsstrukturen in Organismen
- Zellstrukturen und Gewebe
Die Bienenwabe: Perfektion der Natur
Die Bienenwabe ist das perfekte Beispiel für die Effizienz des Sechsecks:
Mathematische Perfektion
- Maximale Fläche bei minimalem Umfang
- Geringster Materialverbrauch (Wachs)
- Perfekte Tesselation ohne Lücken
- Strukturelle Stabilität
Das Bienenwaben-Theorem
- Mathematisch bewiesene Optimalität
- Isoperimetrisches Problem gelöst
- Inspiriert Architektur und Technik
- Vorbild für Leichtbau-Konstruktionen
Anwendungen des regelmäßigen Sechsecks
Regelmäßige Sechsecke finden vielfältige praktische Anwendung:
Technik & Maschinenbau
- Sechskant-Schrauben und -Muttern
- Werkzeuggriffe (Schraubendreher)
- Maschinenbau-Komponenten
- Honeycomb-Sandwich-Bauweise
Architektur & Design
- Fliesen und Bodenbeläge
- Fassaden-Gestaltung
- Strukturelle Leichtbau-Elemente
- Moderne Gebäude-Geometrie
Spiele & Unterhaltung
- Brettspiele mit hexagonalen Feldern
- Strategiespiele (Siedler von Catan)
- Videospiel-Karten (Civilization)
- Puzzles und Legespiele
Wissenschaft & Forschung
- Molekulare Chemie (Benzol-Ring)
- Materialwissenschaften
- Nano-Technologie (Graphen)
- Optik und Photonik
Formeln für das regelmäßige Sechseck (Hexagon)
Flächeninhalt A
Mit √3 ≈ 1.732 (besonders elegant)
Umfang P
Einfach: 6-mal die Seitenlänge
Kurze Diagonale e
Entspricht der Höhe des Hexagons
Lange Diagonale f
Einfach: doppelte Seitenlänge
Innenkreisradius rᵢ
Apothem des Sechsecks
Umkreisradius rₐ
Umkreisradius = Seitenlänge (einzigartig!)
Seitenlänge aus Diagonalen
Rückwärts-Berechnungen
Innenwinkel α
Jeder der 6 Innenwinkel
Rechenbeispiel für ein Hexagon
Gegeben
Gesucht: Alle Eigenschaften des regelmäßigen Sechsecks
1. Grundmaße berechnen
Umfang und Flächeninhalt
2. Radien berechnen
Umkreis- und Innenkreisradius
3. Diagonalen berechnen
Die beiden verschiedenen Diagonallängen
4. Besondere Eigenschaften
Das Hexagon besteht aus 6 gleichseitigen Dreiecken!
Das regelmäßige Sechseck: Perfektion in Natur und Technik
Das regelmäßige Sechseck ist wohl die eleganteste und praktischste aller geometrischen Formen. Es vereint mathematische Schönheit mit funktionaler Perfektion und demonstriert wie keine andere Form das Prinzip der Effizienz in Natur und Technik.
Mathematische Eleganz und einzigartige Eigenschaften
Die mathematischen Eigenschaften des regelmäßigen Sechsecks zeigen bemerkenswerte Eleganz:
- Perfekte Symmetrie: 6-fache Rotations- und Spiegelsymmetrie
- Einzigartige Radius-Eigenschaft: Umkreisradius = Seitenlänge (rₐ = a)
- √3-Beziehungen: Viele Formeln enthalten √3 als eleganten Faktor
- 60°-Geometrie: Zentrumswinkel 60° führt zu gleichseitigen Dreiecken
- Einfache Konstruktion: Mit Zirkel allein konstruierbar
- Perfekte Tesselation: Lückenlose Parkettierung der Ebene
Die Bienenwabe als Vorbild der Perfektion
Das berühmteste Beispiel für die Perfektion des Sechsecks ist die Bienenwabe:
Das Bienenwaben-Problem
Jahrhundertelang rätselte die Mathematik, warum Bienen sechseckige Waben bauen. 1999 bewies Thomas Hales das "Honeycomb Conjecture": Das Sechseck ist die optimale Form für die Raumaufteilung.
Isoperimetrisches Optimum
Bei gegebenem Umfang hat das Sechseck die größte Fläche aller tesselierbaren Formen. Dies minimiert den Wachsverbrauch bei maximaler Honig-Lagerkapazität.
Strukturelle Vorteile
Die 120°-Winkel sind optimal für die Kraftverteilung. Jede Wand trägt gleichmäßig zur Stabilität bei, ohne Materialverschwendung durch Überdimensionierung.
Naturgesetze in Aktion
Bienen "berechnen" nicht - sie folgen physikalischen Gesetzen. Oberflächenspannung und Energieminimierung führen automatisch zur Sechseck-Form.
Technische Anwendungen und moderne Innovation
Die Effizienz des Sechsecks inspiriert moderne Technik und Design:
- Leichtbau-Revolution: Honeycomb-Sandwich-Bauweise in Luft- und Raumfahrt
- Materialwissenschaft: Graphen und hexagonale Kohlenstoff-Gitter
- Mechanik: Sechskant-Schrauben für optimale Kraftübertragung
- Architektur: Strukturelle Effizienz in Fassaden und Tragwerken
- Spiel-Design: Hexagon-Raster für strategische Brettspiele
- Nano-Technologie: Molekulare Strukturen und Selbstorganisation
Sechseck-Geometrie in verschiedenen Wissenschaften
Das Sechseck durchdringt verschiedene Wissenschaftsbereiche:
Chemie und Molekularstruktur
Der Benzolring (C₆H₆) ist das Grundelement der organischen Chemie. Seine hexagonale Struktur verleiht aromatischen Verbindungen besondere Stabilität.
Physik und Kristallographie
Viele Kristallgitter basieren auf hexagonaler Symmetrie. Graphit, Eis und zahlreiche Mineralien zeigen diese bevorzugte Anordnung.
Biologie und Evolution
Nicht nur Bienen - auch andere Organismen nutzen hexagonale Strukturen für Effizienz: Schildkrötenpanzer, Vogelaugen, Pflanzengewebe.
Geologie und Naturphänomene
Giant's Causeway, Säulenbasalt und andere geologische Formationen entstehen durch die natürliche Tendenz zur hexagonalen Struktur.
Zukunftsperspektiven und Innovation
Das Sechseck inspiriert weiterhin moderne Innovation:
- Metamaterialien: Hexagonale Strukturen für neue optische und akustische Eigenschaften
- 3D-Druck: Honeycomb-Infill für Gewichtsoptimierung bei hoher Festigkeit
- Robotik: Hexapod-Roboter nutzen die 6-fache Symmetrie für Stabilität
- Solarenergie: Hexagonale Solarzellen für optimale Flächennutzung
- Urban Planning: Hexagonale Stadtplanung für effiziente Verkehrsflüsse
Zusammenfassung
Das regelmäßige Sechseck steht als Symbol für die perfekte Verbindung von mathematischer Eleganz und praktischer Effizienz. Von der molekularen Ebene bis zu architektonischen Meisterwerken zeigt es, wie Naturgesetze zu optimalen Lösungen führen. Seine einzigartigen Eigenschaften - insbesondere die Beziehung rₐ = a und die perfekte Tesselation - machen es zur "perfekten Form". In einer Welt, die nach Nachhaltigkeit und Effizienz strebt, bleibt das Hexagon ein zeitloses Vorbild für Design und Innovation.
|
|