Sechzehneck (Hexadekagon) berechnen

Rechner und Formeln für regelmäßige Sechzehnecke

Hexadekagon Rechner

Regelmäßiges Sechzehneck

Ein regelmäßiges Hexadekagon hat 16 gleich lange Seiten und 16 gleich große Winkel (157,5°). 16 = 2⁴ (Potenz von 2).

Bekannten Parameter eingeben
Welcher Parameter ist bekannt?
Wert des ausgewählten Parameters
Berechnungsergebnisse
Seitenlänge a:
Umfang P:
Fläche A:
Diagonale d2:
Diagonale d3:
Diagonale d4:
Diagonale d5:
Diagonale d6:
Diagonale d7:
Diagonale d8:
Innenradius ri:
Außenradius ra:

Regelmäßiges Hexadekagon

Das Diagramm zeigt ein regelmäßiges Sechzehneck mit allen relevanten Parametern.
Alle 16 Seiten sind gleich lang, alle Innenwinkel betragen 157,5°.

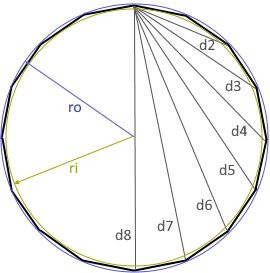
Hexadekagon

Eigenschaften eines regelmäßigen Sechzehnecks

Ein regelmäßiges Sechzehneck (Hexadekagon) ist ein hochsymmetrisches geometrisches Objekt:

  • 16 gleiche Seiten: Alle Seitenlängen sind identisch
  • 16 gleiche Winkel: Jeder Innenwinkel beträgt exakt 157,5°
  • Winkelsumme: 14 × 180° = 2520°
  • Potenz von 2: 16 = 2⁴ - besondere Eigenschaften
  • Zentrumswinkel: 360°/16 = 22,5° pro Segment
  • Konstruktion: Sehr einfach konstruierbar

Das Sechzehneck und binäre Systeme

Das regelmäßige Sechzehneck profitiert von der Potenz-von-2-Eigenschaft:

Binäre Eigenschaften
  • 16 = 2⁴ (4. Potenz von 2)
  • Binär: 10000 (5 Bit)
  • Hexadezimal: 10 (1 Hexadezimalstelle)
  • Einfache Halbierung möglich
Teilbarkeits-Eigenschaften
  • Teilbar durch: 1, 2, 4, 8, 16
  • Symmetrische Unterteilungen möglich
  • Oktogon (8-Eck) als Hälfte
  • Quadrat (4-Eck) als Viertel

Konstruktion und mathematische Eleganz

Das regelmäßige Sechzehneck ist besonders konstruktionsfreundlich:

Einfache Konstruktion
  • Mit Zirkel und Lineal sehr einfach
  • Durch wiederholte Winkelhalbierung
  • 22,5° = 45°/2 = 90°/4
  • Zentrumswinkel exakt konstruierbar
Trigonometrische Werte
  • sin(22,5°) = √(2-√2)/2
  • cos(22,5°) = √(2+√2)/2
  • Exakte algebraische Ausdrücke
  • Einfache Berechnungen möglich

Anwendungen des regelmäßigen Sechzehnecks

Regelmäßige Sechzehnecke finden breite praktische Anwendung:

Navigation & Orientierung
  • Präzise Kompassrosen (22,5° Schritte)
  • Windrichtungsanzeiger
  • Nautische Navigationshilfen
  • Astronomische Instrumente
Architektur & Design
  • Kuppelkonstruktionen
  • Fenstermosaike und Rosetten
  • Bodenbeläge und Fliesenmuster
  • Dekorative architektonische Elemente
Maschinenbau & Technik
  • Hochpräzisions-Zahnräder
  • Lager- und Kupplungsdesigns
  • Rotationssymmetrische Bauteile
  • Werkzeugmaschinen-Komponenten
Digitaltechnik & Computing
  • Encoder-Scheiben (4-Bit Auflösung)
  • Digitale Drehgeber und Sensoren
  • Algorithmus-Design für 2⁴-Strukturen
  • Computergrafik und Game-Design

Formeln für das regelmäßige Sechzehneck (Hexadekagon)

Flächeninhalt A
\[A = 4 \cdot a^2 \cdot \cot\left(\frac{\pi}{16}\right) \approx 20.109 \cdot a^2\]

Mit cot(π/16) ≈ 5.027

Umfang P
\[P = 16 \cdot a\]

Einfach: 16-mal die Seitenlänge

Diagonale d₂
\[d_2 = a \cdot \frac{\sin(2\pi/16)}{\sin(\pi/16)} \approx 1.962 \cdot a\]

Kürzeste Diagonale

Diagonale d₄
\[d_4 = a \cdot \frac{\sqrt{2}/2}{\sin(\pi/16)} \approx 3.625 \cdot a\]

Mit √2/2 (45° Beziehung)

Diagonale d₈ (längste)
\[d_8 = \frac{a}{\sin(\pi/16)} \approx 5.126 \cdot a\]

Durchmesser des Umkreises

Weitere Diagonalen
\[d_3 \approx 2.853 \cdot a\] \[d_5 \approx 4.256 \cdot a\] \[d_6 \approx 4.746 \cdot a\] \[d_7 \approx 5.027 \cdot a\]

Systematische Progression

Umkreisradius rₐ
\[r_a = \frac{a}{2\sin(\pi/16)} \approx 2.563 \cdot a\]

Mit sin(π/16) ≈ 0.195

Innenkreisradius rᵢ
\[r_i = \frac{a \cdot \cot(\pi/16)}{2} \approx 2.514 \cdot a\]

Apothem des Sechzehnecks

Rechenbeispiel für ein Hexadekagon

Gegeben
Seitenlänge a = 5

Gesucht: Alle Eigenschaften des regelmäßigen Sechzehnecks

1. Grundmaße berechnen
\[P = 16 \times 5 = 80\] \[A = 20.109 \times 25 = 502.73\]

Umfang und Flächeninhalt

2. Radien berechnen
\[r_a = 2.563 \times 5 = 12.82\] \[r_i = 2.514 \times 5 = 12.57\]

Umkreis- und Innenkreisradius

3. Alle Diagonalen (Auswahl)
d₂ = 1.962 × 5 = 9.81 d₃ = 2.853 × 5 = 14.27 d₄ = 3.625 × 5 = 18.13
d₅ = 4.256 × 5 = 21.28 d₆ = 4.746 × 5 = 23.73 d₇ = 5.027 × 5 = 25.14 d₈ = 5.126 × 5 = 25.63

Alle sieben verschiedenen Diagonallängen

4. Vollständige Zusammenfassung
Seitenlänge a = 5.00 Umfang P = 80.00 Fläche A = 502.73 Umkreisradius = 12.82
Innenkreisradius = 12.57 Innenwinkel = 157.5° Zentrumswinkel = 22.5° Binär = 10000₂

Komplette Charakterisierung des regelmäßigen Sechzehnecks

Das regelmäßige Sechzehneck in Wissenschaft und Technik

Das regelmäßige Sechzehneck nimmt eine besondere Stellung ein, da es als Potenz von 2 (16 = 2⁴) ideale Eigenschaften für technische Anwendungen und digitale Systeme mitbringt. Diese mathematische Eigenschaft macht es zu einem bevorzugten Element in Precision Engineering und Computersystemen.

Potenz-von-2-Eigenschaften und ihre Vorteile

Die Eigenschaften als 4. Potenz von 2 verleihen dem Sechzehneck einzigartige Vorteile:

  • Binäre Kompatibilität: 16 = 2⁴ entspricht 4 Bits in digitalen Systemen
  • Einfache Teilbarkeit: Durch 1, 2, 4, 8, 16 gleichmäßig teilbar
  • Konstruktive Einfachheit: Zentrumswinkel 22,5° = 90°/4 exakt konstruierbar
  • Symmetrie-Hierarchie: Enthält Quadrat (4), Oktogon (8) als Unterteilungen
  • Rechnerfreundlichkeit: Ideal für algorithmebasierte Berechnungen

Precision Engineering und Messtechnik

In der Präzisionstechnik bietet das Sechzehneck besondere Vorteile:

Encoder-Technologie

16-Position-Encoder bieten 4-Bit Auflösung mit perfekter binärer Darstellung. Jede Position entspricht exakt einem 4-Bit-Code von 0000 bis 1111.

Präzisions-Mechanik

Hochpräzise Zahnräder und Kupplungen nutzen die 16-fache Symmetrie für gleichmäßige Kraftverteilung und minimale Vibration.

Navigation und Orientierung

22,5°-Schritte ermöglichen präzise Richtungsangaben. 16 Richtungen decken alle Hauptrichtungen ab (N, NNE, NE, ENE, etc.).

Mess- und Kalibrierungssysteme

Standard-Referenz für Rundtische, Drehteller und Winkel-Mess-Geräte in der Qualitätssicherung.

Digitale Anwendungen und Algorithmen

Das Sechzehneck findet breite Anwendung in digitalen Systemen:

  • Computergrafik: 16-fache Rotationssymmetrie für 3D-Modelle und Animationen
  • Signal Processing: 16-Punkt-FFT und digitale Filterdesigns
  • Game Design: Bewegungsrichtungen in Spielen (16-Wege-Kontrolle)
  • User Interface: Radiale Menüs mit 16 Optionen für Touch-Interfaces
  • Robotik: Sensorarrays und omnidirektionale Bewegungssteuerung
  • Bildverarbeitung: Template Matching und Objekterkennung

Moderne Fertigungstechnologie

In der modernen Produktion bietet das Sechzehneck praktische Vorteile:

CNC-Bearbeitung

Standard-G-Code-Programme für 16-seitige Bearbeitung. Indexierbare Werkzeugwechsler nutzen oft 16-Position-Magazine.

3D-Druck und Rapid Prototyping

Optimale Balance zwischen Präzision und Druckzeit. 16 Facetten bieten gute Kreisapproximation bei vertretbarem Aufwand.

Qualitätssicherung

Standardisierte Prüfkörper und Referenzobjekte. Koordinatenmessmaschinen verwenden 16-Punkt-Kreismessungen.

Automatisierung

Förderanlagen, Sortiermaschinen und Pick-and-Place-Roboter nutzen 16-fache Teilung für optimale Arbeitsplätze.

Zusammenfassung

Das regelmäßige Sechzehneck repräsentiert die perfekte Verbindung zwischen klassischer Geometrie und moderner Technologie. Seine Eigenschaften als Potenz von 2 machen es zu einem idealen Interface zwischen analoger und digitaler Welt. Von Präzisionsmechanik über Computergrafik bis hin zu modernen Fertigungstechnologien zeigt das Hexadekagon, wie mathematische Eleganz praktische Probleme lösen kann. Es steht als Symbol für die Effizienz, die entsteht, wenn Geometrie und Binärsysteme harmonieren.

Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?

Weitere Polygone

Dreieck • Viereck (Quadrat) • Fünfeck (Pentagon) • Sechseck (Hexagon) • Siebeneck (Heptagon) • Achteck (Oktagon) • Neuneck (Nonagon) • Zehneck (Dekagon) • Elfeck (Hendekagon) • Zwölfeck (Dodekagon) • Sechzehneck (Hexadekagon) • Regelmäßiges N-Eck • Regelmäßigen Vieleckring • Konkaves gleichseitigen Sechseck • Achsensymmetrisches Fünfeck • Verlängertes Sechseck • Verlängertes Achteck • Pentagramm • Hexagramm • Oktagramm • Sterns von Lakshmi