Achsensymmetrisches Fünfeck berechnen
Rechner und Formeln für das symmetrische irreguläre Pentagon
Achsensymmetrisches Fünfeck Rechner
Das achsensymmetrische Fünfeck
Ein achsensymmetrisches Fünfeck ist ein irreguläres Pentagon mit einer Symmetrieachse. Definiert durch 3 Seitenlängen und 1 Winkel.
Pentagon-Struktur
Das achsensymmetrische Fünfeck hat eine vertikale Symmetrieachse.
Definiert durch Basis a, Seiten b, c und Basiswinkel α.
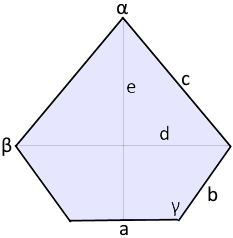
Das achsensymmetrische Fünfeck
Ein achsensymmetrisches Fünfeck ist eine spezielle Form des irregulären Pentagons:
- Eine Symmetrieachse: Vertikal durch die Spitze und Basismitte
- Fünf Seiten: Basis a, zwei Seiten b, zwei Seiten c
- Vier Parameter: Drei Längen und ein Winkel zur vollständigen Bestimmung
- Symmetrische Struktur: Spiegelung an der vertikalen Achse
- Praktische Anwendung: Architektur, Design, Technik
- Berechnung komplex: Trigonometrische Formeln erforderlich
Achsensymmetrie-Eigenschaften
Die Achsensymmetrie verleiht dem Pentagon besondere geometrische Eigenschaften:
Symmetrieachse
- Verläuft vertikal durch das Pentagon
- Teilt die Figur in zwei kongruente Hälften
- Schneidet die Basis a in der Mitte
- Geht durch die gegenüberliegende Spitze
Symmetrische Elemente
- Zwei Seiten der Länge b (symmetrisch)
- Zwei Seiten der Länge c (symmetrisch)
- Gleiche Basiswinkel an beiden Seiten
- Symmetrische Höhen und Diagonalen
Geometrische Analyse
Die geometrischen Eigenschaften des achsensymmetrischen Fünfecks:
Winkelbeziehungen
- α: Basiswinkel (gegeben)
- β: Mittlerer Winkel (berechnet)
- γ: Oberer Basiswinkel (berechnet)
- Summe: 540° (Pentagon-Eigenschaft)
Abstandsbeziehungen
- d: Diagonale (Kosinussatz)
- h: Höhe (Pythagoras-Anwendung)
- U: Umfang = a + 2b + 2c
- A: Fläche (komplexe Formel)
Anwendungen des achsensymmetrischen Fünfecks
Das achsensymmetrische Fünfeck findet vielfältige praktische Anwendungen:
Architektur & Bauwesen
- Hausgiebel und Dachformen
- Fenster- und Türöffnungen
- Dekorative Fassadenelemente
- Kirchenfenster und Rosetten
Maschinenbau & Technik
- Spezielle Werkzeugformen
- Getriebe- und Nockenprofile
- Strukturelle Verstärkungsrippen
- Optische Komponenten
Design & Kunst
- Logo-Design und Corporate Identity
- Möbeldesign und Innenarchitektur
- Schmuck und dekorative Objekte
- Textilmuster und Ornamente
Natur & Biologie
- Blattformen und botanische Strukturen
- Kristallwachstum und Mineralien
- Anatomische Querschnitte
- Biomimetic Design
Formeln für das achsensymmetrische Fünfeck
Diagonale d
Kosinussatz für die Hauptdiagonale
Umfang U
Summe aller fünf Seitenlängen
Höhe h
Summe der Höhenabschnitte mit Pythagoras
Mittlerer Winkel β
Kosinussatz angewendet auf das mittlere Dreieck
Basiswinkel γ
Aus der Pentagon-Innenwinkelsumme
Flächeninhalt A
Komplexe Flächenformel aus zwei Dreiecksanteilen
Rechenbeispiel für ein achsensymmetrisches Fünfeck
Gegeben
Gesucht: Alle geometrischen Eigenschaften des symmetrischen Pentagons
1. Grundberechnungen
Diagonale und Umfang berechnen
2. Winkelberechnung
Mittlere und obere Basiswinkel
3. Höhe und Fläche
Komplexe Berechnungen mit Pythagoras und Flächenformeln
4. Vollständiges achsensymmetrisches Fünfeck
Das vollständige symmetrische Pentagon - eine harmonische geometrische Form
Das achsensymmetrische Fünfeck: Geometrie der Balance
Das achsensymmetrische Fünfeck ist ein faszinierendes Beispiel dafür, wie Symmetrie und Irregularität in der Geometrie koexistieren können. Als Pentagon mit einer einzigen Spiegelachse verbindet es die strukturelle Einfachheit regulärer Formen mit der Flexibilität irregulärer Polygone und findet dadurch vielfältige Anwendungen in Architektur, Design und technischen Konstruktionen.
Symmetrie als Ordnungsprinzip
Die Achsensymmetrie verleiht dem Pentagon besondere Eigenschaften:
- Eine Reflexionsachse: Vertikal durch Spitze und Basismittelpunkt
- Paarsymmetrie: Zwei Seiten b und zwei Seiten c sind jeweils gleich
- Reduzierte Komplexität: Nur 4 Parameter statt 8 bei allgemeinem Pentagon
- Eindeutige Bestimmung: Drei Längen und ein Winkel genügen
- Berechenbare Eigenschaften: Alle anderen Maße folgen aus den Grundparametern
- Ästhetische Balance: Visuell ansprechende, harmonische Proportionen
Mathematische Herausforderungen
Die Berechnung achsensymmetrischer Pentagone erfordert fortgeschrittene Geometrie:
Trigonometrische Methoden
Kosinussatz und Sinussatz ermöglichen die Berechnung unbekannter Seiten und Winkel aus den gegebenen Parametern.
Komplexe Flächenberechnung
Die Fläche erfordert die Zerlegung in Dreiecke und die Anwendung spezieller Flächenformeln.
Höhenbestimmung
Die Gesamthöhe setzt sich aus verschiedenen Höhenabschnitten zusammen, die mit dem Satz des Pythagoras berechnet werden.
Winkelbeziehungen
Die Innenwinkelsumme von 540° (Pentagon-Eigenschaft) ermöglicht die Berechnung unbekannter Winkel.
Praktische Anwendungen in der realen Welt
Das achsensymmetrische Fünfeck findet breite praktische Anwendung:
- Architektonische Giebel: Hausformen mit Pentagon-Silhouette
- Industriedesign: Werkzeuge und Komponenten mit optimierter Funktionalität
- Optische Systeme: Linsen und Prismen mit speziellen Eigenschaften
- Strukturmechanik: Verstärkungsrippen und Trägerelemente
- Verpackungsdesign: Effiziente und ästhetische Behälterformen
- Künstlerische Gestaltung: Logos, Ornamente und dekorative Elemente
Verbindung zu anderen geometrischen Konzepten
Das achsensymmetrische Pentagon verbindet verschiedene geometrische Prinzipien:
Symmetrie-Theorie
Als Beispiel für partielle Symmetrie zeigt es, wie eine einzige Reflexionsachse komplexe Formen ordnet und vereinfacht.
Trigonometrie
Die Anwendung von Sinus-, Kosinus- und Tangens-Funktionen zur Lösung komplexer geometrischer Probleme.
Analytische Geometrie
Koordinatensysteme und algebraische Methoden ergänzen die klassische Euklidische Geometrie.
Optimierung
In technischen Anwendungen oft Grundlage für Optimierungsprobleme bezüglich Fläche, Umfang oder Materialverbrauch.
Zusammenfassung
Das achsensymmetrische Fünfeck steht als eleganter Beweis dafür, dass Symmetrie nicht Perfektion bedeuten muss, sondern vielmehr Balance und Ordnung in der Vielfalt. Seine mathematische Behandlung verbindet elementare Geometrie mit fortgeschrittenen trigonometrischen Methoden und zeigt, wie aus wenigen Grundparametern komplexe Strukturen entstehen können. In einer Welt, die zunehmend nach funktionaler Ästhetik sucht, bietet das achsensymmetrische Pentagon eine perfekte Synthese aus mathematischer Präzision und praktischer Anwendbarkeit. Es lehrt uns, dass wahre geometrische Schönheit nicht in der absoluten Regelmäßigkeit liegt, sondern in der intelligenten Balance zwischen Ordnung und Variation - ein Prinzip, das von der Natur bis zur modernen Architektur immer wieder bestätigt wird.
|
|