Zwölfeck (Dodekagon) berechnen

Rechner und Formeln für regelmäßige Zwölfecke

Dodekagon Rechner

Regelmäßiges Zwölfeck

Ein regelmäßiges Dodekagon hat 12 gleich lange Seiten und 12 gleich große Winkel (150°). Es entspricht den Stunden auf einer Uhr.

Bekannten Parameter eingeben
Welcher Parameter ist bekannt?
Wert des ausgewählten Parameters
Berechnungsergebnisse
Seitenlänge a:
Umfang P:
Fläche A:
Diagonale d2:
Diagonale d3:
Diagonale d4:
Diagonale d5:
Diagonale d6:
Innenradius ri:
Außenradius ra:

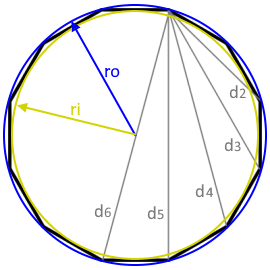
Regelmäßiges Dodekagon

Das Diagramm zeigt ein regelmäßiges Zwölfeck mit allen relevanten Parametern.
Alle 12 Seiten sind gleich lang, alle Innenwinkel betragen 150°.

Dodekagon

Eigenschaften eines regelmäßigen Zwölfecks

Ein regelmäßiges Zwölfeck (Dodekagon) ist ein hochsymmetrisches geometrisches Objekt:

  • 12 gleiche Seiten: Alle Seitenlängen sind identisch
  • 12 gleiche Winkel: Jeder Innenwinkel beträgt exakt 150°
  • Winkelsumme: 10 × 180° = 1800°
  • Uhr-Analogie: 12 Positionen wie Stunden auf einer Uhr
  • Zentrumswinkel: 360°/12 = 30° pro Segment
  • Konstruierbarkeit: Mit Zirkel und Lineal konstruierbar

Das Zwölfeck und die Uhr

Das regelmäßige Zwölfeck hat eine natürliche Verbindung zur Zeitmessung:

Uhrzeiger-Positionen
  • 12 Stunden entsprechen 12 Ecken
  • Zentrumswinkel 30° = 1 Stunde
  • Stundenzeiger dreht sich um 30° pro Stunde
  • Natürliche Orientierungshilfe
Navigationsbezug
  • Kompassrose mit 12 Haupt-Himmelsrichtungen
  • 30° Intervalle für Navigation
  • Historische Windrose-Teilung
  • Maritime und terrestrische Orientierung

Konstruktion und mathematische Eigenschaften

Das regelmäßige Zwölfeck zeigt interessante mathematische Eigenschaften:

Klassische Konstruktion
  • Mit Zirkel und Lineal konstruierbar
  • Über drei- und vierfache Teilung des Kreises
  • Kombination von Dreieck und Viereck
  • Zentrumswinkel: 360°/12 = 30°
Mathematische Werte
  • sin(30°) = 1/2, cos(30°) = √3/2
  • Einfache trigonometrische Verhältnisse
  • Verbindung zu √2 und √3
  • Ganzzahlige Teilbarkeit der Winkelsumme

Anwendungen des regelmäßigen Zwölfecks

Regelmäßige Zwölfecke finden vielfältige praktische Anwendung:

Uhren & Zeitmessung
  • Zifferblätter und Uhrengehäuse
  • Turmuhr-Designs
  • Chronometer und Präzisionsuhren
  • Dekorative Uhren und Wanduhren
Architektur & Kunst
  • Kirchenfenster und Rosetten
  • Kuppelkonstruktionen
  • Gartenanlagen und Brunnen
  • Dekorative Bodenbeläge
Navigation & Orientierung
  • Kompassrosen und Windkarten
  • Nautische Navigationsinstrumente
  • Astronomische Messgeräte
  • Surveying und Vermessungstechnik
Technik & Industrie
  • Maschinenbau: Zahnräder und Kupplungen
  • Elektrotechnik: Steckverbinder
  • Automobilindustrie: Felgen und Räder
  • Optik: Prisma und Linsensysteme

Formeln für das regelmäßige Zwölfeck (Dodekagon)

Flächeninhalt A
\[A = 3(2 + \sqrt{3}) \cdot a^2 \approx 11.196 \cdot a^2\]

Kombination aus Quadraten und Dreiecken

Umfang P
\[P = 12 \cdot a\]

Einfach: 12-mal die Seitenlänge

Diagonale d₂
\[d_2 = \frac{\sqrt{6} + \sqrt{2}}{2} \cdot a \approx 1.932 \cdot a\]

Kürzeste Diagonale

Diagonale d₃
\[d_3 = (\sqrt{3} + 1) \cdot a \approx 2.732 \cdot a\]

Mit √3 und 1

Diagonale d₄
\[d_4 = \frac{3\sqrt{2} + \sqrt{6}}{2} \cdot a \approx 3.347 \cdot a\]

Kombination von √2 und √6

Diagonale d₅ (Höhe h)
\[d_5 = h = (2 + \sqrt{3}) \cdot a \approx 3.732 \cdot a\]

Längste Diagonale = Höhe

Diagonale d₆
\[d_6 = (\sqrt{2} + \sqrt{6}) \cdot a \approx 3.864 \cdot a\]

Maximale Diagonale

Innenkreisradius rᵢ
\[r_i = \frac{(2 + \sqrt{3}) \cdot a}{2} \approx 1.866 \cdot a\]

Halbe Höhe d₅

Umkreisradius rₐ
\[r_a = \frac{\sqrt{6} + \sqrt{2}}{2} \cdot a \approx 1.932 \cdot a\]

Entspricht Diagonale d₂

Rechenbeispiel für ein Dodekagon

Gegeben
Seitenlänge a = 10

Gesucht: Alle Eigenschaften des regelmäßigen Zwölfecks

1. Grundmaße berechnen
\[P = 12 \times 10 = 120\] \[A = 11.196 \times 100 = 1119.6\]

Umfang und Flächeninhalt

2. Radien berechnen
\[r_a = 1.932 \times 10 = 19.32\] \[r_i = 1.866 \times 10 = 18.66\]

Umkreis- und Innenkreisradius

3. Alle Diagonalen
d₂ = 1.932 × 10 = 19.32 d₃ = 2.732 × 10 = 27.32 d₄ = 3.347 × 10 = 33.47
d₅ = h = 3.732 × 10 = 37.32 d₆ = 3.864 × 10 = 38.64

Alle fünf verschiedenen Diagonallängen

4. Vollständige Zusammenfassung
Seitenlänge a = 10.00 Umfang P = 120.00 Fläche A = 1119.60 Höhe h = 37.32
Umkreisradius = 19.32 Innenkreisradius = 18.66 Innenwinkel = 150° Zentrumswinkel = 30°

Komplette Charakterisierung des regelmäßigen Zwölfecks

Das regelmäßige Zwölfeck in Theorie und Praxis

Das regelmäßige Zwölfeck nimmt eine besondere Stellung unter den Polygonen ein, da es eine perfekte Balance zwischen geometrischer Einfachheit und praktischer Anwendbarkeit darstellt. Seine Verbindung zu unserem Zeitsystem und zur Navigation macht es zu einem der kulturell bedeutsamsten geometrischen Formen.

Mathematische Eleganz und Konstruktion

Die mathematischen Eigenschaften des regelmäßigen Zwölfecks zeigen besondere Eleganz:

  • Einfache Konstruktion: Als 3×4 oder 4×3 Teilung des Kreises sehr zugänglich
  • Bekannte trigonometrische Werte: sin(30°) = 1/2, cos(30°) = √3/2
  • Kombinatorische Eigenschaften: Vereint Eigenschaften von Dreieck und Viereck
  • Symmetrie: 12-fache Rotations- und Spiegelsymmetrie
  • Teilbarkeit: Durch 2, 3, 4 und 6 gleichmäßig teilbar

Kulturelle und praktische Bedeutung

Die praktische Bedeutung des Zwölfecks zeigt sich in vielen Bereichen:

Zeitsysteme

Von antiken Sonnenuhren bis zu modernen Chronometern - das Zwölfeck prägt unser Zeitverständnis durch die 12-Stunden-Teilung des Tages.

Navigation

Kompassrosen und Navigationsinstrumente nutzen die 12-teilige Struktur für präzise Richtungsangaben in 30°-Schritten.

Architektur

Kirchenfenster, Kuppeln und Gartenanlagen verwenden das Zwölfeck als harmonisches Gestaltungselement.

Technik

Maschinenbau und Elektrotechnik schätzen die gleichmäßige Verteilung für Zahnräder, Steckverbinder und rotationssymmetrische Bauteile.

Moderne Anwendungen und Zukunftsperspektiven

In der modernen Technik gewinnt das Zwölfeck neue Bedeutung:

  • CAD/CAM-Systeme: Standardform für rotationssymmetrische Bauteile und Werkzeuge
  • Robotik: 12-teilige Sensor- und Aktuator-Arrays für omnidirektionale Bewegung
  • Optik: Apertur-Designs und Prisma-Systeme nutzen die 12-fache Symmetrie
  • Nanotechnologie: Molekulare Strukturen mit 12-facher Symmetrie
  • Energietechnik: Windkraft- und Solaranlagen mit optimaler Raumaufteilung
Zusammenfassung

Das regelmäßige Zwölfeck vereint mathematische Eleganz mit kultureller Bedeutung und praktischer Anwendbarkeit. Seine Verbindung zu Zeit und Navigation, die einfache Konstruierbarkeit und die harmonischen Proportionen machen es zu einer zeitlosen geometrischen Form. Von antiken Sonnenuhren bis zu modernen Hochpräzisions-Instrumenten zeigt das Dodekagon die dauerhafte Relevanz klassischer Geometrie in einer technologisierten Welt.

Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?

Weitere Polygone

Dreieck • Viereck (Quadrat) • Fünfeck (Pentagon) • Sechseck (Hexagon) • Siebeneck (Heptagon) • Achteck (Oktagon) • Neuneck (Nonagon) • Zehneck (Dekagon) • Elfeck (Hendekagon) • Zwölfeck (Dodekagon) • Sechzehneck (Hexadekagon) • Regelmäßiges N-Eck • Regelmäßigen Vieleckring • Konkaves gleichseitigen Sechseck • Achsensymmetrisches Fünfeck • Verlängertes Sechseck • Verlängertes Achteck • Pentagramm • Hexagramm • Oktagramm • Sterns von Lakshmi