Konkaves Hexagon berechnen
Rechner und Formeln für konkave Sechsecke
Konkaves Hexagon Rechner
Konkaves Sechseck
Ein konkaves Hexagon ist gleichseitig aber nicht regelmäßig. Mindestens ein Innenwinkel > 180° macht es konkav.
Konkaves Hexagon
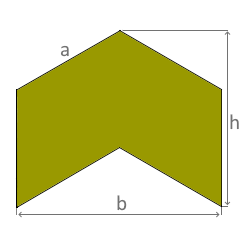
Das Diagramm zeigt ein gleichseitiges konkaves Sechseck.
Alle 6 Seiten sind gleich, aber die Winkel sind unterschiedlich.
Was ist ein konkaves Sechseck?
Ein konkaves Sechseck unterscheidet sich grundlegend vom regulären Hexagon:
- Gleichseitig: Alle 6 Seiten sind gleich lang
- Nicht regulär: Die Winkel sind unterschiedlich
- Konkavität: Mindestens ein Innenwinkel > 180°
- Einwärts gebogen: Form "stülpt sich ein"
- Sternförmige Silhouette: Charakteristische Form
- Spezielle Geometrie: Einzigartige Eigenschaften
Geometrische Eigenschaften
Das konkave Hexagon zeigt faszinierende geometrische Eigenschaften:
Winkel-Eigenschaften
- Winkelsumme: (6-2) × 180° = 720°
- Mindestens ein Winkel > 180° (konkav)
- Andere Winkel können < 180° sein
- Ungleiche Winkelverteilung
Maß-Beziehungen
- Alle Seiten: a (gleichseitig)
- Breite: b = √3 · a
- Höhe: h = 1.5 · a
- Kompakte, sternförmige Gestalt
Mathematische Beziehungen
Das konkave Hexagon folgt spezifischen mathematischen Gesetzen:
Flächenberechnung
Die Fläche entspricht 2/3 der Fläche eines regulären Hexagons mit gleicher Seitenlänge.
Proportionen
Das Verhältnis von Breite zu Höhe ist konstant und ergibt sich aus der geometrischen Konstruktion.
Anwendungen konkaver Hexagone
Konkave Hexagone finden spezialisierte Anwendungen:
Design & Kunst
- Moderne Logogestaltung
- Architektonische Akzente
- Dekorative Kunst-Objekte
- Grafische Muster und Ornamente
Technische Anwendungen
- Spezial-Werkzeuge und -Schlüssel
- Maschinenbau-Komponenten
- Optische Blenden (spezielle Form)
- Puzzle und Spielkomponenten
Spieledesign
- Strategiespiele mit besonderen Feldern
- Puzzle-Komponenten
- Dekorative Spielbrett-Elemente
- 3D-Druck Modelle
Wissenschaft
- Geometrische Studien
- Mathematische Modellierung
- Computergrafik-Algorithmen
- Topologische Untersuchungen
Formeln für das konkave Sechseck
Flächeninhalt A
Bemerkenswert einfache Formel mit √3
Umfang P
Wie beim regulären Hexagon
Breite b
Horizontale Ausdehnung
Höhe h
Vertikale Ausdehnung
Seitenlänge a (aus Fläche)
Rückwärts-Berechnung
Verhältnis zu regulärem Hexagon
Interessante geometrische Beziehung
Rechenbeispiel für ein konkaves Hexagon
Gegeben
Gesucht: Alle Eigenschaften des konkaven Sechsecks
1. Grundmaße berechnen
Umfang und Flächeninhalt
2. Abmessungen berechnen
Breite und Höhe
3. Vergleich mit regulärem Hexagon
Das konkave Hexagon ist flächensparender
4. Vollständige Zusammenfassung
Charakteristikum: Sternförmige, nach innen gewölbte Gestalt
Das konkave Hexagon: Geometrische Besonderheit
Das konkave Hexagon ist eine faszinierende geometrische Form, die zeigt, wie sich durch Variation der Winkel bei gleich bleibenden Seitenlängen völlig neue Eigenschaften ergeben. Es steht als Beispiel für die Vielfalt geometrischer Möglichkeiten jenseits der regulären Formen.
Definition und grundlegende Eigenschaften
Ein konkaves Polygon ist dadurch charakterisiert, dass mindestens einer seiner Innenwinkel größer als 180° ist:
- Konkavität: Mindestens ein Innenwinkel > 180° (Reflexwinkel)
- Gleichseitigkeit: Alle sechs Seiten haben die gleiche Länge
- Nicht-Regularität: Die Winkel sind nicht alle gleich
- Sternform: Die Form "stülpt sich nach innen ein"
- Einfache Verbindung: Trotz Konkavität einfach verbunden
Mathematische Analyse der besonderen Geometrie
Das konkave Hexagon zeigt interessante mathematische Beziehungen:
Flächenverhältnisse
Die Fläche beträgt genau √3 · a², was 2/3 der Fläche eines regulären Hexagons entspricht. Diese elegante Beziehung ergibt sich aus der spezifischen Winkelverteilung.
Proportionalität
Das Verhältnis von Breite zu Höhe (√3 : 1.5) ist konstant und unabhängig von der Größe, was charakteristisch für diese geometrische Form ist.
Symmetrie-Eigenschaften
Obwohl nicht regulär, besitzt das konkave Hexagon spezielle Symmetrien. Es hat eine vertikale Spiegelachse und zeigt 2-fache Rotationssymmetrie.
Konstruktive Aspekte
Die Konstruktion erfolgt durch gezieltes "Einwärtsbiegen" zweier gegenüberliegender Bereiche eines regulären Hexagons bei Beibehaltung der Seitenlängen.
Anwendungen in Design und Technik
Trotz ihrer Spezialisierung findet das konkave Hexagon praktische Anwendungen:
- Industriedesign: Spezialwerkzeuge mit ungewöhnlichen Griffformen
- Architektur: Dekorative Elemente mit besonderer Ästhetik
- Kunst und Grafik: Logos und Symbole mit "eingestülpter" Charakteristik
- Spieledesign: Puzzleteile und Spielkomponenten mit Wiedererkennungswert
- 3D-Druck: Objekte, die sowohl kompakt als auch visuell interessant sind
Geometrische Verwandtschaften und Variationen
Das konkave Hexagon steht in Beziehung zu anderen geometrischen Formen:
Reguläres Hexagon
Das reguläre Hexagon kann als "Grenzfall" betrachtet werden, bei dem alle Winkel 120° betragen. Das konkave Hexagon entsteht durch Vergrößerung bestimmter Winkel über 180° hinaus.
Sterne und Sternpolygone
Es zeigt Verwandtschaft zu Sternformen, allerdings ohne sich selbst zu schneiden. Es kann als "einwärts gerichteter Stern" interpretiert werden.
Andere konkave Polygone
Als Vertreter der konkaven Polygone zeigt es charakteristische Eigenschaften dieser Formklasse: reduzierte Fläche bei gleichen Seitenlängen.
Topologische Eigenschaften
Trotz Konkavität bleibt es einfach verbunden und zeigt, wie lokale Formänderungen globale Eigenschaften beeinflussen können.
Zusammenfassung
Das konkave Hexagon demonstriert die Vielfalt geometrischer Formen jenseits der bekannten regulären Polygone. Seine eleganten mathematischen Beziehungen - insbesondere die √3-Faktoren und das 2/3-Flächenverhältnis - zeigen, wie geometrische Variation zu neuen, aber dennoch harmonischen Proportionen führt. Es steht als Beispiel dafür, dass auch ungewöhnliche Formen mathematisch beschreibbar sind und praktische Anwendungen finden können. In einer Welt, die zunehmend nach einzigartigen Designlösungen sucht, bietet das konkave Hexagon eine interessante Alternative zu konventionellen Formen.
|
|