Unregelmäßiges Sechseck berechnen
Rechner und Formeln für das verlängerte Hexagon
Unregelmäßiges Sechseck Rechner
Das unregelmäßige Sechseck
Ein unregelmäßiges Sechseck ist ein verlängertes Hexagon mit zwei verschiedenen Seitenlängen aber gleichen Innenwinkeln von 120°.
Sechseck-Struktur
Das unregelmäßige Sechseck hat zwei verschiedene Seitenlängen.
Alle Innenwinkel betragen einheitlich 120°.
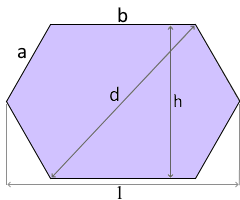
Das unregelmäßige verlängerte Sechseck
Das unregelmäßige Sechseck ist eine spezielle Form des Hexagons mit besonderen Eigenschaften:
- Sechs Seiten: 4 Seiten der Länge a, 2 Seiten der Länge b
- Gleiche Winkel: Alle Innenwinkel betragen 120°
- Verlängerte Form: Rechteckiger Mittelteil mit 60°-Abschrägungen
- Einfache Berechnung: Nur zwei Parameter erforderlich
- √3-Mathematik: Höhe h = a·√3 (60°-Trigonometrie)
- Praktische Form: Häufig in Design und Technik verwendet
120°-Winkel-Eigenschaften
Die Winkel-Struktur des unregelmäßigen Sechsecks basiert auf der 60°-Geometrie:
Innenwinkel
- Alle 6 Innenwinkel = 120°
- Summe: 6 × 120° = 720°
- Entspricht der Hexagon-Formel: (6-2) × 180°
- 30° mehr als rechter Winkel
Außenwinkel
- Alle 6 Außenwinkel = 60°
- Summe: 6 × 60° = 360°
- Entspricht der allgemeinen Polygon-Regel
- Fundamental für equilaterale Dreiecke
√3-Geometrie und Struktur
Die geometrische Struktur des verlängerten Sechsecks:
Aufbau-Prinzip
- Mittelteil: Rechteck der Größe b × h
- Seitenteile: 2 Parallelogramme
- Ecken: 4 equilaterale Dreiecke (60°)
- Symmetrie: Horizontal symmetrisch
√3-Mathematik
- Höhe: h = a·√3
- Länge: l = a + b
- √3 ≈ 1.732: Fundamental für 60°-Geometrie
- Elegante Formeln: Einfache Beziehungen
Anwendungen des unregelmäßigen Sechsecks
Das verlängerte Sechseck findet vielfältige praktische Anwendungen:
Industrie & Technik
- Schraubenkopf-Profile (verlängerte Sechskante)
- Spezielle Werkzeugformen
- Rohrleitungs-Verbindungsstücke
- Getriebe- und Maschinenbauteile
Architektur & Design
- Fenster- und Türformen
- Fliesen- und Bodenbelag-Muster
- Säulen- und Strukturprofile
- Dekorative Wandelemente
Design & Kunst
- Logo-Design und Corporate Identity
- Möbeldesign und Tischformen
- Schmuck und dekorative Objekte
- Textilmuster und Ornamente
Natur & Biologie
- Kristallstrukturen und Mineralien
- Bienenwaben-ähnliche Strukturen
- Molekulare Geometrie
- Biologische Zellstrukturen
Formeln für das unregelmäßige Sechseck
Länge l
Einfache Addition der beiden Seitenlängen
Höhe h
Höhe basiert auf 60°-Trigonometrie
Umfang U
4 kurze Seiten plus 2 lange Seiten
Diagonale d
Pythagoras angewendet auf Höhe und lange Seite
Flächeninhalt A
Hexagon-Anteil plus Rechteck-Verlängerung
√3-Konstante
Fundamental für 60°-Winkel-Geometrie
Innenwinkel
Alle Innenwinkel sind gleich groß
Rechenbeispiel für ein unregelmäßiges Sechseck
Gegeben
Gesucht: Alle geometrischen Eigenschaften des verlängerten Sechsecks
1. Grundmaße berechnen
Höhe mit √3 und einfache Längensumme
2. Umfang und Diagonale
Gesamtumfang und Hauptdiagonale
3. Flächenberechnung
Zusammensetzung aus Hexagon-Anteil und Rechteck-Verlängerung
4. Vollständiges unregelmäßiges Sechseck
Das vollständige verlängerte Sechseck - elegante √3-Mathematik trifft praktisches Design
Das unregelmäßige Sechseck: √3-Geometrie trifft Design
Das unregelmäßige verlängerte Sechseck ist ein elegantes Beispiel dafür, wie die natürliche √3-Geometrie der 60°-Winkel mit praktischen Designanforderungen kombiniert werden kann. Als Hexagon mit zwei verschiedenen Seitenlängen, aber einheitlichen 120°-Innenwinkeln, verbindet es die Harmonie der Bienenwaben-Struktur mit der Flexibilität funktionaler Formgebung und findet dadurch breite Anwendung von der Industrie bis zur Kunst.
Die Magie der √3-Geometrie
Die Besonderheit des verlängerten Sechsecks liegt in seiner √3-basierten Mathematik:
- 120°-Innenwinkel: Perfekte 60°-Außenwinkel schaffen equilaterale Dreiecke
- √3-Höhe: h = a·√3 ≈ 1.732·a aus der 60°-Trigonometrie
- Natürliche Proportionen: Entspricht der Kristallstruktur vieler Mineralien
- Einfache Formeln: Trotz √3 mathematisch sehr handhabel
- Modular erweiterbar: Rechteckige Verlängerung durch Parameter b
- Bienenwaben-Verwandtschaft: Basis-Geometrie der effizientesten Naturstrukturen
120° - Der perfekte Kompromiss
Der einheitliche Innenwinkel von 120° macht dieses Hexagon besonders wertvoll:
Natürliche Harmonie
120° ist der Innenwinkel des regelmäßigen Sechsecks - die gleiche Geometrie, die Bienenwaben ihre optimale Raumaufteilung verleiht.
Kristallographie
Viele Kristallstrukturen basieren auf 120°-Winkeln, von Quarz bis zu Schneeflocken - eine fundamentale Ordnung der Natur.
Technische Vorteile
120°-Winkel sind mechanisch stabil und ermöglichen gleichmäßige Kraftverteilung - ideal für Konstruktionsanwendungen.
Ästhetische Wirkung
Die Kombination aus scharfen 120°-Winkeln und fließenden Übergängen schafft eine ausgewogene visuelle Spannung.
Vielseitige Anwendungsfelder
Das verlängerte Sechseck findet Anwendung in überraschend vielen Bereichen:
- Schraubentechnik: Verlängerte Sechskantschrauben für spezielle Anwendungen
- Architektur: Fensterformen und strukturelle Profile
- Möbeldesign: Tische und Arbeitsplatten mit funktionaler Eleganz
- Fliesentechnik: Parkett- und Bodenbelag-Muster
- Kristallzucht: Wachstumsformen für synthetische Kristalle
- Optik: Linsen- und Prismengeometrie für spezielle Anwendungen
Von der Natur lernen: Biomimetik
Das verlängerte Sechseck zeigt, wie Biomimetik funktioniert:
Bienenwaben-Prinzip
Die hexagonale Grundstruktur maximiert das Volumen bei minimalem Materialverbrauch - ein Optimierungsprinzip der Evolution.
Kristalline Ordnung
Die 120°-Winkel entsprechen den energetisch günstigsten Anordnungen in der Materie - von Atomen bis zu Galaxien.
Technische Umsetzung
Moderne Werkstoffe wie Honeycomb-Strukturen und Metamaterialien nutzen diese Geometrie für Leichtbau und Festigkeit.
Design-Innovation
Von Tesla-Batteriezellen bis zu Smartphone-Displays - die hexagonale Geometrie optimiert Funktionalität und Ästhetik gleichermaßen.
Zusammenfassung
Das unregelmäßige verlängerte Sechseck vereint die Weisheit der Natur mit den Anforderungen moderner Technik und Gestaltung. Seine √3-basierte Mathematik spiegelt die fundamentalen Ordnungsprinzipien des Universums wider, während seine praktische Anwendbarkeit von Schraubenköpfen bis zu Kristallstrukturen reicht. Die einheitlichen 120°-Winkel schaffen strukturelle Stabilität und ästhetische Harmonie, während die variable Verlängerung funktionale Flexibilität ermöglicht. In einer Welt, die sowohl Effizienz als auch Schönheit sucht, zeigt das verlängerte Sechseck, dass die besten Lösungen oft die einfachsten sind - mathematisch elegant, technisch praktikabel und visuell ansprechend. Es erinnert uns daran, dass wahre Innovation nicht darin liegt, die Natur zu überwinden, sondern ihre zeitlosen Prinzipien intelligent zu adaptieren und für menschliche Bedürfnisse nutzbar zu machen.
|
|