Achteck (Oktagon) berechnen
Rechner und Formeln für regelmäßige Achtecke
Oktagon Rechner
Regelmäßiges Achteck
Ein regelmäßiges Oktagon hat 8 gleich lange Seiten und 8 gleich große Winkel (135°). 8 = 2³ (Potenz von 2).
Regelmäßiges Oktagon
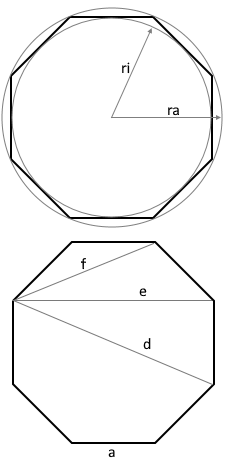
Das Diagramm zeigt ein regelmäßiges Achteck mit allen relevanten Parametern.
Alle 8 Seiten sind gleich lang, alle Innenwinkel betragen 135°.
Eigenschaften eines regelmäßigen Achtecks
Ein regelmäßiges Achteck (Oktagon) ist eine der symmetrischsten geometrischen Formen:
- 8 gleiche Seiten: Alle Seitenlängen sind identisch
- 8 gleiche Winkel: Jeder Innenwinkel beträgt exakt 135°
- Winkelsumme: 6 × 180° = 1080°
- Potenz von 2: 8 = 2³ - besondere Eigenschaften
- Zentrumswinkel: 360°/8 = 45° pro Segment
- Konstruktion: Einfach konstruierbar
Das Achteck und binäre Systeme
Das regelmäßige Achteck profitiert von der Potenz-von-2-Eigenschaft:
2³-Eigenschaften
- 8 = 2³ (3. Potenz von 2)
- Binär: 1000 (4 Bit)
- Oktalsystem: Basis 8
- Einfache Halbierung möglich
Teilbarkeits-Eigenschaften
- Teilbar durch: 1, 2, 4, 8
- Quadrat (4-Eck) als Hälfte
- 45°-Winkel sind exakt darstellbar
- Stop-Schild Form (bekannt weltweit)
Geometrische Eleganz und Konstruktion
Das regelmäßige Achteck zeigt besondere geometrische Eleganz:
Einfache Konstruktion
- Mit Zirkel und Lineal konstruierbar
- 45°-Winkel sind exakt konstruierbar
- Zentrumswinkel: 360°/8 = 45°
- √2-Beziehungen in allen Formeln
Mathematische Werte
- sin(45°) = cos(45°) = √2/2
- tan(45°) = 1
- sin(22,5°) = √(2-√2)/2
- Alle Werte exakt darstellbar
Anwendungen des regelmäßigen Achtecks
Regelmäßige Achtecke haben breite praktische Anwendung:
Verkehr & Sicherheit
- Stop-Schilder (international genormt)
- Verkehrszeichen und Warntafeln
- Sicherheits- und Hinweisschilder
- Industrielle Kennzeichnung
Architektur & Bauwesen
- Achteckige Türme und Pavillons
- Fenster und Oberlichter
- Fliesen und Bodenbeläge
- Gartenpavillon und Gazebos
Technik & Industrie
- Maschinenbau-Komponenten
- Schraubenköpfe und Muttern
- Lager und Kupplungen
- Präzisionswerkzeuge
Spiele & Design
- Brettspielelemente
- Puzzle und Denkspiele
- Grafik-Design und Logos
- Dekorative Kunst-Objekte
Formeln für das regelmäßige Achteck (Oktagon)
Flächeninhalt A
Elegante Formel mit √2
Umfang P
Einfach: 8-mal die Seitenlänge
Lange Diagonale d
Durchmesser des Achtecks
Mittlere Diagonale e
Doppelter Innenkreisradius
Kurze Diagonale f
Kleinste der drei Diagonalen
Umkreisradius rₐ
Halbe lange Diagonale
Innenkreisradius rᵢ
Apothem des Achtecks
Alternative Flächenformel
Über Umkreisradius
Rechenbeispiel für ein Oktagon
Gegeben
Gesucht: Alle Eigenschaften des regelmäßigen Achtecks
1. Grundmaße berechnen
Umfang und Flächeninhalt
2. Radien berechnen
Umkreis- und Innenkreisradius
3. Alle drei Diagonalen
Kurze, mittlere und lange Diagonale
4. Vollständige Zusammenfassung
Das perfekte Achteck für Verkehrsschilder und Architektur
Das regelmäßige Achteck: Symbol der Ordnung
Das regelmäßige Achteck ist wohl das bekannteste aller Polygone, da es als Stop-Schild täglich millionenfach auf der ganzen Welt wahrgenommen wird. Doch hinter dieser Alltäglichkeit verbirgt sich eine mathematisch elegante Form mit besonderen Eigenschaften und vielfältigen Anwendungen.
Die Macht der Acht: 2³ und seine Bedeutung
Die Zahl 8 als dritte Potenz von 2 verleiht dem Achteck besondere mathematische Eleganz:
- Binäre Perfektion: 8 = 2³ entspricht exakt 3 Bits in digitalen Systemen
- 45°-Geometrie: Zentrumswinkel 45° = 90°/2 - perfekt konstruierbar
- √2-Beziehungen: Alle Formeln enthalten √2 als eleganten Faktor
- Stop-Schild Universalität: Weltweit als "STOP" erkannt
- Architektonische Tradition: Jahrtausendealte Verwendung in der Baukunst
Das Stop-Schild: Globales Symbol der Ordnung
Die berühmteste Anwendung des Achtecks ist das internationale Stop-Schild:
Historische Entwicklung
1915 in den USA entwickelt, setzte sich das achteckige Stop-Schild aufgrund seiner einzigartigen Form durch. Kein anderes Verkehrszeichen hat diese charakteristische 8-Eck-Form.
Psychologische Wirkung
Die 8 Ecken und die rote Farbe signalisieren sofort "Gefahr" und "Stopp". Selbst bei schlechter Sicht ist die achteckige Silhouette sofort erkennbar.
Internationale Standardisierung
Das Wiener Übereinkommen über Straßenverkehrszeichen machte das achteckige Stop-Schild zum weltweiten Standard. Form vor Sprache!
Praktische Vorteile
Auch von hinten erkennbar, wind- und wetterstabil, einfach zu produzieren und zu montieren. Die perfekte Verbindung von Geometrie und Funktion.
Architektonische Tradition und moderne Anwendungen
Das Achteck hat eine reiche architektonische Geschichte und moderne Anwendungen:
- Klassische Architektur: Baptisterien, Kapellen und Zentralbauten
- Islamische Kunst: Oktogonale Muster in Moscheen und Palästen
- Moderne Architektur: Wohntürme, Bürogebäude und Pavillons
- Garten- und Landschaftsarchitektur: Gazebos, Brunnen und Aussichtstürme
- Industriedesign: Maschinenbauteile, Schrauben und Verbindungselemente
- Digitale Welt: Icons, Logos und User Interface Elemente
Mathematische Eleganz und praktische Berechnungen
Die mathematischen Beziehungen im Achteck zeigen besondere Schönheit:
√2-Familie
Alle Achteck-Formeln basieren auf √2 und seinen Potenzen. Die Fläche 2a²(1+√2) zeigt die elegante Verbindung zwischen Seitenlänge und Wurzelausdrücken.
Drei Diagonaltypen
Kurze (f), mittlere (e) und lange Diagonale (d) stehen in harmonischen Verhältnissen und ermöglichen vielseitige konstruktive Anwendungen.
45°-Symmetrie
Der 45°-Zentrumswinkel macht das Achteck zu einem der konstruktionsfreundlichsten Polygone. Rechte Winkel lassen sich exakt halbieren.
Praktische Berechenbarkeit
Trotz der √2-Ausdrücke sind alle Werte mit einfachen Taschenrechnern gut approximierbar und praktisch verwendbar.
Zusammenfassung
Das regelmäßige Achteck vereint mathematische Eleganz mit praktischer Funktionalität wie kaum eine andere geometrische Form. Als Stop-Schild ist es das wohl bekannteste Polygon der Welt und rettet täglich Leben durch seine eindeutige Erkennbarkeit. Seine Eigenschaften als 2³ machen es ideal für technische Anwendungen, während die √2-Beziehungen mathematische Schönheit offenbaren. Von antiken Baptisterien bis zu modernen Verkehrssystemen zeigt das Achteck, wie Geometrie Kultur, Sicherheit und Ästhetik verbinden kann. Es steht als Symbol für Ordnung, Sicherheit und die perfekte Balance zwischen Einfachheit und Eleganz.
|
|